Field Theoretic Phase Space

FIELD THEORETIC PHASE SPACE

AS A CLUE TO AVOID THE REDUCTIONISM

YOSHIDA, Nobuo

Although phase space plays a crucial role in various areas of science, it is usually regarded as nothing more than a mathematical tool. In this paper the idea is proposed that the field theoretic phase space, but not the four dimensional coordinate space, is real. The 'scarred' wave function, which is known to appear in the quantized chaotic system, is interpreted as real construct in the physical world. This interpretation is useful in avoiding the pitfall of the reductionism. The conjecture concerning the subjectivity problem is also presented.

1.Introduction

Revolutionary ideas based on the phase space formulation have attracted much research interest in more than twenty years; frequently quoted terms are 'catastrophe', 'self-organization', 'cooperative phenomenon', and 'chaos'. Thus, it is recognized that the phase space is useful to depict both qualitative and quantitative behavior of complicated systems, but most researchers regard it as a mere mathematical tool and do not admit its physical reality. After the radical change of the world view brought about in the first half of this century, however, we can hardly find any evidence against the reality of the phase space.
The classical view of the physical world is: In the rigid three dimensional space there exists some physical entity (matter) that varies with the lapse of time. This 'space-time-matter' schema was rejected by modern physicists on the basis of the following reasons: (1) The theory of general relativity converted the concept of rigid empty space and continuously passing time into that of the four dimensional manifold. (2) The quantum theory of field revealed that ordinary 'matter' such as crystal or polymer is not a self-supporting object, but a coherently excited state of field variables each assigned to definite space-time point. Such a drastic change of world view prompts us to reinvestigate the physical role of ordinary four dimensional coordinate space and value-taking variables of matter fields.
In this paper I propose the idea that the high-dimensional phase space embracing quantum field variables possesses the genuine physical reality, while the four dimensional coordinate space does not (Sec.2-3). 'Scarred' structure of a wave function that represents a definite quantum history of a chaotic system is interpreted as real construct in the phase space (Sec.4-5). Since, according to the scientific methodology, whether an object mentioned in the literature is real or not is out of the question so far as its notion is efficient in explaining physical phenomena, the implication of this idea mainly concerns philosophical arguments; it elucidates the ontological status of 'whole' and 'parts', and thus offers us a clue to avoid falling into the pitfall of the annoying atomistic reductionism (Sec.6). Furthermore, I make a comment on the possible relation between the physical entity and the conscious self (Sec.7), which may intrigue the philosophers interested in the mind-bodyproblem.

2.Phase Space in Field Theory

In classical mechanics, time evolution of a dynamical system is usually formulated in phase space, which is defined as a 2n-dimensional cartesian space formed of generalized coordinates q₁...q_n and their conjugate momenta p₁...p_n. Time evolution is specified by one of the one-dimensional, non-intersecting trajectories, which represent the set of solutions of the Hamilton's equation of motion. In modern physics, however, such a formulation is inadequate because of the requirement of relativity and the quantum uncertainty principle. Since we have not yet developed a systemic formulation of a general relativistic quantum field theory on the basis of genuine dynamical variables, we should be satisfied with a 'toy model' which mimics the essential features of the presumed 'true' theory. In the following I adopt a hypercubic lattice field theory as the toy model, which offers a guiding principle of the phase space formulation.
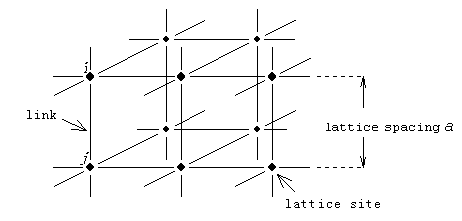
A lattice field theory is defined on a discrete lattice instead of space-time continuum, and is usually considered as an approximation of a continuum theory, the lattice spacing being an ultraviolet cut-off (see as a review Kogut 1979). The rigorous way to construct it is quite cumbersome due to the constraint of so-called gauge invariance (Wilson 1974); for example, matter (e.g., quark or lepton) field and force (e.g.,gauge boson) field variable should be placed on a site and a link of a lattice, respectively (Fig.1). Here, in order to avoid unessential complexity, we restrict ourselves to the scalar field φ_i, which is defined on each lattice site i and has no internal degree of freedom. The interaction term of the action integral is supposed to be written as

S = Σ_i,e g(e) φ_i・φ_ｅ・i ,

where e・i denotes the site of the interacting partner of φ_i, and g(e) is the coupling constant that may depend on the relative position of the partner.

In ordinary formulation, the lattice is embedded in three or four dimensional coordinate space. However, such embedding is redundant, because, once the lattice structure is determined in a definite way, any physical phenomenon can be simulated by the lattice dynamics only, and the space surrounding the lattice is never referred to anymore.
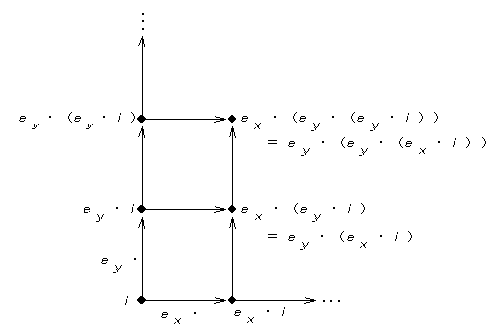
As a matter of fact, hypercubic lattice can be constructed mathematically without any mention of the Euclidean coordinate. A generator e is defined as the operator on a lattice which designates the site of the interacting partner according to the interaction term. Suppose that there are four distinctive generators {e_x,e_y,e_z,e_t} and their inverses {e_x^-1,..}, which obey the linear operation laws such as commutative or associative laws (e_x・ e_y= e_y・ e_x,.., e_x・ (e_y・ e_z)=(e_x・ e_y)・ e_z, .. ). Then, the whole hypercubic lattice, which is an analog of the four dimensional coordinate space, is generated as a linear space on integer with the basis {e_t,e_x,e_y,e_z} (Fig.2). Note that here the non-local property has been implicitly introduced through the imposition of the linear operation laws.

In a more realistic formulation, the interacting pair should be interconnected by force field variable placed on a link of lattice. Probably gravitational field changes the length of link between each site so that the whole lattice would become amorphous, which corresponds to the actual situation of this universe.
It is inferable from these that what we call coordinate space is an approximate representation of mathematical structure of the interaction network among dynamical variables. In stead of the artificial coordinate space, we should admit the reality of space formed of dynamical variables {φ_i}, which will be called 'phase space' in the following.

3.Cognitive Processing and Artificiality of Coordinate Space

At a first glance, it may seem improbable that the coordinate space, which appears with intuitive reality in our daily experience, would be artificial. In this section, I present, with the help of the cognitive science, the argument against this objection.
As Piaget and Inhelder pointed out (1967), the concept of Euclidean metric derives from topological ideas and appears at a later stage in the psychological development of a child. Contrary to the ordinary view, the intuition of geometrical space is not 'direct perceptual apprehension of the external world', but consists of more complex operations including both processing of sense-data and regulation of motor activity.
Experimental data of neurophysiology suggest that the ability to perform these psychological operations is acquired in accord with the organization of certain cortical circuits through perceptual and behavioral experiences. For example, in the visual cortex of a kitten reared in an artificial environment consisting entirely of vertical (horizontal) stripes during the critical period, the optimal orientations for neurons that respond to elongated stimuli show anisotropic distribution concentrating upon the vertical (horizontal) (Blakemore and Cooper 1970); such a kitten conceivably has difficulty in getting the intuition of the extension perpendicular to the orientation it has experienced.
In general synaptic connections in sensorium of a normal animal are arranged during postnatal development so as to extract useful information on circumstances from the firing pattern of sensory neurons. The obtained information is efficient if utilizable from the viewpoint of the adaptive strategy, and does not necessarily simulate the external faithfully.
For the description of kinematical features of a moving object, coordinate space is more convenient than phase space because of easiness of parametric representation. In fact, direction of a motion at a given instance can be determined by only two angular parameters in three dimensional Euclidean coordinate space, whereas, in phase space, dynamical variables incorporated into that motion are too numerous to select a few as characteristic parameters. Thus, it seems probable thatneural circuits, organized to process the sufficient information for survival within the limited capacity of cognition, generate the intuitive notion of coordinate space as cognitive artefact.

4.Complemented History of Quantum System

In classical mechanics which requires the single-valuedness of individual physical quantity, the whole history of a system shrinks to a single point in the phase space. Causal property of the motion equation restricts the points corresponding to physically realizable histories to the region with null measure.
Quantization procedure abolishes this restriction. To make clear the relation to the ordinary formulation of quantum mechanics, I use the wave function 'at each time', i.e., in the case of hypercubic lattice, the function of dynamical variables on lattice sites (t_i, x_j) where time t_i is fixed. The wave function is written as

Ψ（φ(t_i, x₁), φ(t_i, x₂), ..., φ(t_i, x_k), ...）,

or, in abbreviated notation, as

Ψ（t_i；φ₁,φ₂, ..., φ_k, ...）,

which can be interpreted as the configuration-space representation of a state vector ｜Ψ(t)〉.
A method for describing the 'history' of a quantum system without referring to 'conscious observers' or 'instantaneous decay of wave packets' was developed by Griffiths (1984), and subsequently elaborated by Omnes (1989) and Gell-Mann and Hartle (1991). Their results can be summarized, with intentional simplification in some controversial points, as follows. For an isolated quantum system with definite initial state ｜Ψ₀〉 at t=T₀, it is possible to choose, at a certain time T_j, a full set of mutually exclusive projectors {P_aj(T_j),P_bj(T_j),..} (expressed in the Heisenberg picture), each of which projects the state vector on one branch of decohering process.
A time evolution sequence is obtained by successively operating the projectors P_a1(T₁), ...,P_bi(T_i), ... on
｜Ψ₀〉, where T₀<T₁<..<T_i<...
Since interference terms are cancelled out when the celebrated 'consistency conditions' are satisfied, each sequence is interpreted as a physically realizable 'history', to which is assigned the classical joint probability.
Although there is a wide-spread belief that we cannot tell anything about the transitional state, it is convenient for our purpose to introduce the interpolating state ｜Ψ(t)〉 (in the Schrodinger picture) that contains the entire information of the system in the course of a certain history. ｜Ψ(t)〉 is identical with the initial state ｜Ψ₀〉at t=T₀, and simulates the 'historical' fact at the instance of decohering, i.e.,

P_bi｜Ψ(T_i)〉 = ｜Ψ(T_i)〉

(for P_bi that determines the history),

P_ci｜Ψ(T_i)〉 = 0

(for other projectors).

During the intermediate period ｜Ψ(t)〉 remains in principle arbitrary except the requirement of smoothness.
In the phase space formulation, a history complemented with the interpolating state is represented by the set of wave functions covering all sites of lattice ｛Ψ(t₀；..,φ_k,..),...,Ψ(t_i；..,φ_k,..),...｝, which will be referred to as a 'time-dependent wave function', or simply as a 'wave function'. Fig.3 shows a schematic example in the case with only two variables at each time, where the squared amplitude is depicted as the density of dots.

The significance of a quantum wave function is as yet unclear, but since quantum fluctuation has actual effects such as the spontaneous decay of classically stable nucleus, it is reasonable to assume that the value of each dynamical variable is not uniquely determined, but is distributed over some range. At the present stage a quantum wave function is the only available quantity that contains information on the fluctuation of dynamical variables, and hence we may provisionally admit its physical reality. It is likely that truly realistic quantity will be introduced in the future; even to this case the following discussion is applicable only with slight modification, so far as the quantity is expressed as a function of dynamical variables.

5.'Scarred' Structure of Wave Function

Although the classical trajectory of, say, an electron in a Hydrogen atom is obscured by quantization procedure, there is a quantum analogue that mimics the phase trajectory of a dissipative system. For instance, calculations based on a simple model show that collective coordinates weakly coupled with its environment approximately obey, after decoherence has taken place, the classical motion equation with the dissipation term (Feynmann and Vernon 1963). This result indicates that the notion of 'attractor' is useful in investigating the collective behavior of the system.
Generally speaking, a regular system exhibits smooth collective motion; wave packet moves along a classical trajectory for a while, and　asymptotically approaches a certain stable state that corresponds to a sink or a limit cycle in the unquantized case.
In an irregular, or chaotic, quantum system, the deformation of wave packet is much more complicated. In this case many of the quantum eigenfunctions show distinctive structure with high amplitude zone along some classical periodic trajectories, as if they had 'scars' (Hellar 1984; see also as a review Jensen 1992). The corresponding classical trajectories are not necessarily stable, and so they do not coincide with limit cycles. Nevertheless, when the system is embedded in an environment weakly coupled with it, the 'scarred' eigenfunction represents an equilibrium state that is actualized through dissipative process. As a consequence, the time-dependent wave function that properly depicts the history leading to some equilibrium shows gradual enhancement of the 'scars'. Accordingly, the central region of a 'scar' is interpreted as a quantum version of an attractor.

6.How to Avoid the Reductionism

In this and the next section I discuss the most fascinating property of the phase space formulation. First, it is shown that the so-called whole and parts problem can be solved.
From the 'reductionistic' point of view, any phenomenon in the physical world could be understood in terms of the local interaction among constituents, which are occasionally identified with elementary particles such as quarks and gluons. Adopting this view, we are led to the conclusion that the notion denoting some system as a whole, e.g., 'a body of an individual' or 'an ecosystem on the earth', is artificial in the sense that it is arbitrarily introduced for the purpose of thinking. Physical reality should be attributed only to the fundamental processes carried out by elementary constituents.
The pseudo-scientific reductionism of this kind, however, has no theoretical justification. It should be emphasized that, according to the quantum field theory, elementary particles are not point-like objects, but merely mathematical expression of base vectors used for perturbative expansion. The most typical case to which the particle picture is applicable is a hard scattering process; the incoming or outgoing asymptotic state is expressed, in practice, by a plane wave of a renormalized (viz, externally non-interacting) field, which propagates like a particle with definite velocity. On the contrary, the particle picture is not valid in the strong coupling regime where perturbative expansion diverges; in fact, an electron in a superconductor bears no resemblance to a billiard ball-like particle except that the total number is conserved.
The field theoretic phase space formulation enables us to get a holistic view; it does not allow the existence of an indivisible entity as a constituent of the physical world, except a field variable itself. Like a phase trajectory in classical mechanics, 'scarred' structure of the wave function discussed in the previous section represents a factual phenomenon in a certain history.
Although the phase space itself does not differentiate field variables according to their function, it is convenient to introduce the hierarchical parametrization in order to avoid the complexity due to the gigantic dimensionality of the space. In an ordinary dynamical system with numerous degrees of freedom, the macroscopic, collective behavior is governed by relatively few parameters called order parameters (as a review, see Haken 1978). Mathematically, they are defined as slowly varying parameters which determine the value of 'slave' variables in the adiabatic approximation. Usual cooperative phenomena including biological morphogenesis and other self-organizing processes imply that a non-trivial attractor of a phase trajectory is present in the order parameter space.
This hierarchical parametrization is useful in our formulation. Consider a subspace of N dynamical variables ｛φ₁,…,φ_N｝ where N is a large number. Then, perform the coordinate transformation (with appropriate Jacobian) corresponding to the introduction of order parameters:

｛φ₁,…,φ_N｝ → ｛Q₁,…,Q_f,q₁,…,q_N-f｝,

where f is much smaller than N. This procedure is validated if the wave function shows clumped distribution or uncorrelated fluctuation around the value of each 'slave' variable q which is essentially determined by Q's, or in a rough expression,

Ψ（…,Q_i,…,…,q_j≠q_j(Q),…）≫ 0.

When this condition is satisfied, collective behavior of an individual object is approximately described by the use of order parameter Q's, and so we are allowed to adopt the abbreviated notation Ψ（…,Q_i,…）. In case of the realistic system that embraces macroscopic, cooperative phenomenon such as biological morphogenesis, the 'scarred' structure is expected to appear around the non-trivial quantum attractor, which determines the low dimensional space of order parameters.
This feature is the key to solve the philosophical 'whole and parts' problem. A reductionist may insist that the 'whole' of a system is an artificial notion invented for intellectual thinking. But in the phase space formulation we can visualize the 'whole', which manifests itself through the collective motion, as the characteristic structure of the wave function only by ignoring the irrelevant variables; there is no need to elaborate a theory for modelling the postulated 'whole'. The 'whole' has physical reality in this sense.
One may be sceptical of the physical reality of, for example, an individual of an animal as a whole, because its body is composed of biological tissues, which are further composed of high molecules, of atoms, and ultimately of elementary particles. This scepticism is not supported by field theoretic view. On the contrary, the phase space formulation reveals that, beginning with elementary field, one can proceed to the notion of atoms, high molecules, tissues, and finally the whole body only through the reduction of the number of dimensions. In the ordinary environment on the earth, most field variables are near the ground (vacuum) state, and interesting phenomenon originating from quantum excitation is approximately described in terms of collective motion that conforms to atomic structure. Furthermore, atoms do not behave randomly in an organism; they are assembled through vital reaction to build up, say, biomolecules, which correspond to (approximate) attractors in the parameter space that exhibits the motion of atoms. When we concentrate our attention upon the 'biomolecule' space, we find other cooperative phenomena in higher orders. For instance, collective motion towards low-energy state causes the bilayer structure of lipid molecules, and consequently promotes the formation of a cell membrane; thus, a cell in an organism is physical substance actualized as a scar of the wave function. In this way we can go on reducing the number of dimensions of the phase space until we get to the notion of a whole body. As is easily guessed, however, in the case of a system made up of weakly interacting constituents such as an ecosystem on the earth, the scarred structure becomes so obscure that the reality of the 'whole' becomes questionable.

7.Ghost in the Phase Space

Although the objective world seems to form a unity governed by universal laws of physics, it contains many creatures, each of which presumably has its own subjective world closed by itself. This section is devoted to this philosophical puzzle.
A nervous system usually shows collective activity involving numerous but restricted degrees of freedom. As Hodgkin and Huxley insisted in their pioneering work, the firing of each neuron is a cooperative phenomenon, whose order parameters are the amplitude of membrane potential and the concentrations of several ions. Researchers are used to adopt reduced parameters such as binary (on/off) variables for neural state or electroencephalogram (EEG) activities at various points, which also can be interpreted as approximate order parameters. Cooperative phenomena in a nervous system are governed by attractors in the space formed of these parameters. For instance, in a properly organized neural network model with both excitatory and inhibitory synapses, external stimulus in a certain range often causes, posterior to a transient period, self-sustaining excitation of a partial circuit, which is a sign of a limit cycle.
In recent years particular attention has been paid to a strange (chaotic) attractor that generates the so-called chaos and permits the quick response to the change of environment. Skarda and Freeman (1987) demonstrated, on the basis of the EEG experiment and the computer simulation, that the activity of the olfactory system of a rabbit shows the characteristic behavior of chaos under appropriate conditions. Chaotic system contains an infinite number of unstable fixed points, and the phase trajectory occasionally converges to and diverges from these points (see, for example, Ott 1993). Since our psychological state, too, is unstable and fluctuates around various thoughts as is comprehended through introspection, it is reasonable to assume that cranial nervous system behaves chaotically as a whole, although there remains the possibility that random forces from the external might be essential to the pliant mental operation. It follows from this assumption that the wave function of brain has a scar that corresponds to a strange attractor in the parameter space.
Here I propose a simple hypothesis: The attractor actualized as scarred structure of the wave function is the subjective world. In Section 4 I have justified the assertion that the quantum wave function has physical reality. Consequently, it is in principle permissible to identify its part with the subjective world, which we directly feel real. On the other hand, the objective world with spatial and temporal dimensions is an artefact constructed through the cognitive processing (as discussed in Section 3).
On the basis of this hypothesis, we get a clue to the aforementioned question: Why is one's subjective world (presumably) closed without any boundary that divides the self from the non-self, whereas in the objective world there coexist numerous brains, each bounded by membrane? The reason is that order parameters involved in different nervous systems are mutually decoupled in the sense that the wave function can be written in the multiplicative form as,

Ψ（Q_i(1),…,Q_j(2),…）

　　≫Ψ(1)（Q_i(1),…）・Ψ(2)（Q_j(2),…）,

where upper suffix designates a certain nervous system. Metaphorically speaking, each subject gets a monopoly of his or her own parameter space, and occupies it exclusively. It should be noted that, since order parameters for a cranial nervous system are composed of field variables in restricted region of space and time, one's consciousness is also confined to that region, which is referred to as 'now and here'.
I want to state two more conjectures in the hope of stimulating further discussions:
(1) It seems probable that the degree of awareness which we can evaluate intuitively is physically determined by the Hausdorf dimension of the corresponding attractor and the strength of the coupling between parameters involved. This conjecture is consistent with the empirical knowledge that the dominant contribution to the content of consciousness arises from the associative process in the prefrontal area, which connects various information with each other, including sensory information of higher order, motor programme generated in the motor area, and signals from the brain stem.
(2) There is a controversial question whether a computer has its subjective world or not. Concerning a consecutive sequence computer built up with silicon chips, the answer is definitely 'No', because the electron flow that actualizes the function of computation is driven by the external source of electricity, and does not show cooperative behavior.

References

Blakemore, C. and Cooper, G.P.(1970), "Development of the Brain Depends on the Visual Environment", Nature 228:477-478.
Feynmann, R. and Vernon, F.L.(1963), "The Theory of a General Quantum System Interacting with a Linear Dissipative System", Annals of Physics 24:118-173.
Gell-Mann, M. and Hartle, J.B.(1991), "Alternative Decohering Histories in Quantum Mechanics", in K.K.Phua and Y.Yamaguchi (eds.), Proceedings of the 25th International Conference on High Energy Physics vol.II. Singapore: World Scientific.
Griffiths, R.(1984), "Consistent histories and the Interpretation of Quantum Mechanics", Journal of Statistical Physics 36:219-272.
Jensen, R.V.(1992), "Quantum Chaos", Nature 355:311-318.
Haken, H.(1978), Synergetics－An Introduction. 2nd.ed. Berlin: Springer-Verlag.
Heller, E.J.(1984), "Bound-State Eigenfunctions of Classically Chaotic Hamiltonian Systems", Physical Review Letters 53: 1515-1518.
Kogut, J.B.(1979), "An Introduction to Lattice Gauge Theory and Spin Systems", Reviews of Modern Physics 51: 659-713.
Omnes, R.(1989), "From Hilbert Space to Common Sense", Annals of Physics 201: 354-447.
Ott, E.(1993), Chaos in Dynamical Systems. Cambridge: Cambridge University Press.
Piaget, J. and Inhelder, B.(1967), The Child's Conception of Space.
Translated from the French by F.J.Langdon & J.L.Lunzer. New York: Norton Library.
Skarda, C.A. and Freeman, W.J.(1987), "How Brains Make Chaos in order to Make Sense of the World", Behavioral and Brain Sciences 10: 161-195.
Wilson, K.G.(1974), "Confinement of Quarks", Physical Review D10: 2445-2459.