量子系を記述する状態関数は、２種類の質的に異なる情報を含んでいる。１つは、ある物理量の測定を行ったときに特定の値が得られる確率で、系についての人間の知識に依存する。スリットを通過した１電子の状態関数は円柱面状に拡がって、スクリーン上のある位置に到達する確率を与えるが、輝点が生じて位置についての知識が確定すると、位置の固有状態に“収縮”する。もう１つは、系の量子揺らぎに関する情報で、系の物理的な状態を近似的に指示している。超伝導に関するＢＣＳ理論では、反対の運動量を持つ２つの電子がフォノン相互作用を通じてクーパー対を形成するとされ、その振舞いはボソン的な準粒子としてコヒーレント状態関数で記述される1)。マイスナー効果などを通じて超伝導状態にあることが確認されている金属について物理学者が語るときには、確かな事実であるかのようにクーパー対に言及するのが常である。物理学者にとって、クーパー対の分布などは確率的であるとしても、ペアの形成自体は確定した物理状態なのである。このように、直接的な観測を行っていないにもかかわらず、状態関数の一部が物理状態を確定的に記述すると見なされているケースは数多い2)。
状態関数に２種類の情報が入り混じっていることは、実験の予測など物理学に必要な計算を遂行する上では何の支障もないものの、存在論的な議論を行おうとするときに、さまざまな混乱の元になる。際限なく拡がっていく自由電子の状態関数を、物理的実在と直接には結びつかない確率振幅として扱うことに問題はないが、クーパー対のような準粒子の形成を示す状態関数には、単なる確率振幅とは言い切れないリアリティが感じられる。しかし、超伝導体における電子の状態関数そのものに物理的実在性を認めようとすると、標準的な解釈と齟齬をきたすことは明らかである。物理的システムに関する存在論を展開するためには、状態関数の確率情報と物理情報を分けて取り扱えるような手法を開発することが望ましい。
この論文では、量子過程を互いに干渉しない素過程に分割することによって、状態関数から確率情報を分離する方法を示す。素過程への分割そのものは、Griffiths - Omnès - GellMann - Hartleらによる量子論的な「履歴(history)」3)のアイデアを経路積分の手法に適用した単純な作業にすぎず、物理学的な新しさはない。しかし、「履歴」に関する研究が、主に、近似的に古典論理が適用できる領域の抽出を目的としているのに対して、著者の意図は、確率情報だけを分離することにより、量子論の特殊性を明確に示す物理情報を抜き出すことにある。
ただし、議論を明確にするために、対象とする物理系を有限自由度・有限状態の閉鎖系に限定してある。有限自由度という制限は、場の量子論に応用する際にも、時空を無限分割しないことを意味するが、現行の実験における空間解像度はせいぜい10-1５ｍ程度でしかないため、この制限によって現実性が失われることはない。また、状態数が有限という制限は、経路積分を使って素過程を定義するために必要なもので、これも実験的な解像度の有限性を考慮すれば、充分に現実的な仮定である。さらに、閉鎖系という条件によって、観測者や測定機器があるとしても、系内部に含まれ量子力学に従う対象として扱われる。
ここで、経路積分によって量子過程を表すやり方を簡単に示しておく。
量子力学の一般論に従って、ある時刻における系の状態は、力学的変数q={q1,q2,q3…}の適当な台の上で定義されるノルムが有界な複素線形関数空間のベクトル|ψ>（ないし、その共役ベクトル<ψ|）で表すことにする4)。力学的変数として、各空間点に分配された場の変数を選んでおけば、以下の議論は相対論的量子力学（場の量子論）にも適用できる。それぞれ密度行列ρiとρf (Trρi=Trρf=1)によって定義される時刻ti の始状態から時刻tf の終状態に至る量子過程の遷移確率Tfi は、時間発展のユニタリー演算子Uを使って、次式で与えられる。
Tfi = Tr(ρfU(tf-ti)ρiU†(ti-tf)) …(1)
始状態・終状態として純粋状態を仮定すれば、(1)式は、
Tfi = <f|U(tf-ti)|i><i|U†(ti-tf)|f>
という馴染み深い形になる。始状態・終状態として密度行列を考えるのは、きわめて多数の自由度を有する系の場合、長波長揺らぎの個々のモードを物理的に区別することが難しいため、密度行列によって定義される混合状態を選ぶ方が現実的だからである。多くの実験では、測定される対象を限定しており、それ以外の状態がどうなっているかは見ていないので、始状態・終状態は、測定対象の状態を|ψ>、他の部分に関する恒等演算子をIeとして、
ρ = |ψ><ψ|ÄIe
という形で表される。
(1)式の遷移確率を経路積分法の表式で書き換えるには、各演算子の間に1=∫|q>dq<q|を挟み込み5)、Uの期待値を次式で表せばよい6)（本稿では、表記を簡単にするために、一貫して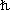
=c=1という自然単位系を用いる）。
<qf|U|qi> = Σall path exp(iS) …(2)
ただし、Sはqiとqfを両端とする１つの経路に対する作用積分
S = ∫dtL （L：ラグランジアン）
で、標準的な理論では対応する古典系の作用積分の式と一致する。なお、(2)式の形を見ると、経路積分というよりも経路和なる呼称の方が適当なので、これ以降は、実際の計算に際しては「経路和」、フォーマリズムを指すときには「経路積分」と使い分けることにする。(2)式を使えば、(1)式の遷移確率は、次のように表される。
Tfi = ∫dq…<|ρf|>(Σall path exp(iS))<|ρi|>(Σall path exp(iS)) …(3)
ただし、式を見やすくするために、変数qの表記は省略し、各qについての積分を∫dq…と略記した。
連続理論の場合、作用積分は時間の関数として表される無数の曲線（多自由度の場合は超曲面）の汎関数となり、全ての可能な経路の和（Σall path）を数学的に正しく定義することは難しい。このため、通常は、始状態から終状態に至る時間を等間隔に区切り、各時刻ごとに変数qについて適当な測度を付けて積分した上で、時間間隔εを小さくするという近似が用いられる。こうした近似の正当性は、経路積分法で求めた答えが、シュレディンガー方程式を解いて得た結果と一致するかどうかで判定される。しかし、複雑な系の場合、シュレディンガー方程式を解くことは一般に困難であり、その助けを借りずに経路和を正しく定義することが望ましい。また、少なからぬ物理学者は、相対論的な共変性が明確な経路積分法こそ系の物理的実態に即した計算法であり7)、根元的な理論が完成した暁には、数学的に破綻のない定義が可能になると信じている。もちろん、現時点では根元的な理論を利用することはできないので、本稿では、次善の策として、対象を有限自由度・有限状態の系に限ることにより、経路和が数学的に正しく定義されているものとする。
有限性の条件によって、(2)式は次のように理解される。
２番目の項目は、たちの悪い超越関数であるexp(iS)が計算に現れないことを意味する。(2)式で指数関数が現れるのは、時間間隔εを最終的にゼロにするという仮定の下で
1+iεL → exp(iεL)
という置き換えを行っているからであり、時空の無限分割を行わない有限自由度の理論では、作用積分が指数の肩に乗ることはない8)。
通常の定式化では、U|i>が|i>を始状態としてシュレディンガー方程式に従って変化する状態関数（q表示をした場合にはψ(q)=<q|U|i>）と見なされ、測定によって|f>という結果が得られる確率振幅は、内積<f|U|i>で与えられるとされる。しかし、この立場を採用すると、始状態と終状態の取り扱いが非対称であり、始状態は系の初期条件として定まっている一方、終状態は測定操作の結果として決定されるかのように見える。これに対して、経路積分法では、始状態と終状態はどちらもあらかじめ与えられたものとして同等に扱われるので、対象を外部からの操作が加えられない閉鎖系に限定したときの記述に適している。経路積分法で<q|U|i>に相当する状態関数を定義するには、ある時刻tの変数だけを固定し、それ以外の変数について経路の足し上げを実行してしまえば良い。(2)式でこの足し上げを実行すると、次の項が残る：
古典論では、作用積分が最小になる経路だけが運動方程式を満たす解軌道として実現されるのに対して、量子論では、さまざまな経路が遷移確率に大なり小なり寄与している。しかも、これらの経路を、確率を計算するために仮想的に導入された統計的集団と見なすことはできない。(1)式にUとU†が現れることから明らかなように、遷移確率には経路積分が２度現れており、異なる経路の交差項（いわゆる干渉項）が寄与することもあるため、個々の経路自体は現実的な物理的過程としての独立性を持っていないからである。１つの遷移過程に多数の経路が寄与することが、経路積分における量子揺らぎの現れである。
鞍点近似が良い精度で成り立つ場合には、作用積分が最小になる古典解が最大の寄与を与え、そこから離れるにつれて経路和への寄与は相対的に抑制されるので、古典解の周りに量子揺らぎが集中しているという解釈が許される（図１）。一方、束縛状態にある粒子では、古典解の軌道よりも特定の周期軌道に対応する経路が大きな寄与を与えるので、古典解とは全く異なる「揺らぎを伴った量子軌道」（例えば水素原子の2p軌道）を想定しなければならない。
(1)，(2)式を使った量子過程の表現は、量子揺らぎを直観的にわかりやすい形で表してはいるものの、このままでは、物理的に区別可能な過程を混ぜ合わせてしまっているため、現実に生起する物理過程と同一視することはできない。例えば、ヤングの二重スリットの実験で光子による干渉縞を観測する場合、始状態として１光子が入射される状態を、終状態として光子が観測装置に到達する状態を考えることが多いが、この設定では、スリットの側の微視的状態が変化することによって干渉性が失われる過程も、同一の量子過程の中に含まれてしまう（詳しくは、次節の例を参照）。現実的な量子過程を考えるためには、互いに干渉しあわない経路のグループごとに分割しなければならない。次に、この方法について議論しよう。
「互いに干渉しあわない」という条件は、干渉項が完全に相殺される「整合性条件」として、すでにGriffithsによって与えられている10)。ここでは、射影演算子を使って量子過程を分割するGriffithsの定式化を、経路積分法における経路のグループ分けとして書き直すことにしよう。
整合性条件によって互いに干渉しあわない量子過程に分割するために、まず、(2)式の右辺で、足し合わせる経路をP1とP2というグループに分ける：
Σall path exp(iS) = ΣP1 exp(iS) + ΣP2 exp(iS) …(5)
経路積分のグループ分けは、自発的対称性の破れなどによって複数の古典解があるときには一般的に使われる技法で、多くの場合は、（図１に示したような）古典解近傍の経路だけを考慮する近似を用いる。ここでは、古典解の有無によらず、任意のグループ分けを想定し、全経路はどちらかのグループに属するものとする。このとき、遷移確率(1)は、次のように書き直される：
Tfi = ∫dq…<|ρf|>(ΣP1exp(iS)+ΣP2exp(iS))<|ρi|>(ΣP1exp(-iS)+ΣP2exp(-iS)) …(6)
ここで、経路積分の形で表した整合性条件：
Re {∫dq…<|ρf|>ΣP1exp(iS)<|ρi|>ΣP2exp(-iS)} = 0 …(7)
が“厳密に”成り立つならば、(6)式を展開したときの交差項（２つのグループの干渉項）は完全に相殺され、遷移確率は経路のグループごとに与えられる正数の和になる：
Tfi = ω1 + ω2
ただし、
ωk = ∫dq…<|ρf|>ΣPkexp(iS)<|ρi|>ΣPkexp(-iS) …(8)
ωkの正値性は、密度行列が正係数cjを使ってΣ|j>cj<j|と展開できることから明らかである。(8)式は、経路がPkに制限された量子過程Ωkを表す。
整合性条件の成否についてコメントしておく。(7)式には指数関数が含まれているので、有限理論の場合、左辺の値を表式のまま評価すると、厳密に0になるとは考えにくい。したがって、前節で述べたように、exp(iS)は形式的な表現で、実際には有限積として評価されるいう制限を付けることが必要である11)。
(5)式のグループ分けが、状態空間の特定の領域を指定する射影演算子によって行えるならば、Ωkは、Griffithsらが議論している量子論的な「履歴」の実例になる12)。例えば、ある時刻に特定の変数Qについて、Qの正負を判定するような測定装置が系に含まれているとしよう。この場合、その時刻において、Q>0またはQ<0のどちらの範囲を通るかという条件で経路のグループ分けが可能になるが、これは、
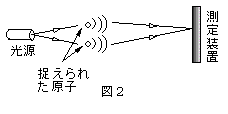
E = ∫Q<0 |Q>dQ<Q|
1-E = ∫Q>0 |Q>dQ<Q|
という２つの排他的射影演算子を挿入することによって「履歴」を定義することに相当する。一般に、射影演算子だけを使ってグループ分けができるとは限らないが、理想化されたケースでは、特定の終状態への射影によって経路が分割できる。
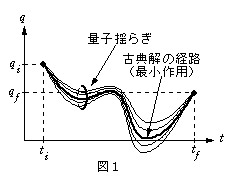
簡単な例として、レーザー冷却法でトラップした２個の原子による光の散乱を考えてみよう。図２のような装置を用いると、二重スリットを用いたヤングの干渉実験と同じ原理によって、干渉パターンが観測される。しかし、散乱を引き起こす原子の状態によっては、干渉パターンは“なまった”ものになる。
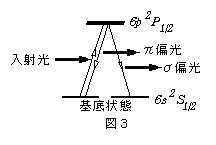1993年にEichmannらが行った実験13)では、基底状態が２重に縮退している水銀原子に特定の励起状態に遷移させる波長の紫外光を照射することによって、散乱後の原子状態が始状態と同一になってπ偏光の散乱波を放射するケース１と、始状態とは磁気量子数が異なる状態に遷移してσ偏光の散乱波を放射するケース２に分けることができた（図３）。ケース１では、２つの原子のいずれによって散乱されたかが決定されないため、各原子によるπ偏光の散乱波同士が干渉して、通常の干渉縞が観測される。しかし、ケース２の場合は、磁気量子数の変化を調べることによってどちらの原子が光を散乱させたかが決定できるので、σ偏光の散乱波は干渉を起こさない14)。実際、偏光状態を識別できる測定装置によってσ偏光の散乱波だけを集めると、干渉縞のないパターンが得られることが、Eichmannらによって実験的に確かめられた。偏光状態を調べる測定装置を用いない場合は、２種類のパターンが重なって、強弱の度合いが低減した（なまった）干渉縞が生じる。
この例では、「入射された１個の光子が原子に散乱された後に測定装置に到達する」という量子過程が、(1)原子状態が変わらず、散乱後の光子がπ偏光となる経路、(2)上の原子の状態が変わり、光子がσ偏光となる経路、(3)下の原子の状態が変わり、光子がσ偏光となる経路──という互いに干渉しない３つのグループに分割される。原子状態を区別しない遷移確率の計算では、原子の終状態として２つの基底状態の混合を考えるのが一般的だが、ここで述べたような経路のグループ分けは、原子の終状態を基底状態の一方に射影することによって得られる。一般に、始状態や終状態として混合状態を選んだとしても、それが物理的に区別できるものであるならば、この例ように、干渉し合わない純粋状態間の遷移に分割される。
上の議論を一般化して、任意の量子過程Ωを素過程に分割する手順をまとめよう。
経路の総数をNとして15)、全ての経路に1からNまでのナンバーを振ることにする。１つの経路pnに対する作用積分をSnとし、次のN×N行列を考える：
Rnm = {∫dq…<|ρf|>exp(iSn)<|ρi|>exp(-iSm) + c.c. }/2 …(9)
(9)式より、Rnmは実対称行列（Rnm*=Rnm=Rmn）である。(3)式と比較すれば直ちにわかるように、遷移確率は、
Tfi = Σn,m Rnm
となる。また、経路のナンバリングの変更は、N次の置換行列Cを使って、CRCTと表される。
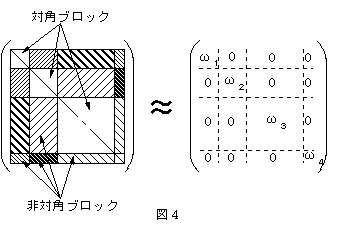
整合性条件(7)は、「適当なCを使ってRが擬対角化される」という形で一般化できる。ただし、擬対角化行列とは、図４の斜線を付けた非対角ブロック内の行列要素の和がゼロになる行列である。有限行列の行と列の置換は有限の手続きで行えるため、Rから作られる擬対角化行列を枚挙することは原理的に可能である。
ある擬対角化行列のブロック分けに対応する経路のグループ（総数J個）を、順にP1,P2,…Pk,…,PJとする(1≦J≦N)。グループPkによって指定される対角ブロック内部の行列要素の和は、(8)式で定義される正数ωkとなり、このブロック全体が、経路がPkに制限された量子過程Ωkを表している。
あるRに対する擬対角化行列は複数個存在し得るが、その中でJが最大になるものを考える。このとき、各対角ブロックが表す量子過程Ωkの経路を、整合性条件を満たすグループにさらに分割することは、Jが最大という条件より不可能である。したがって、このΩkを（それ以上分割できないと言う意味で）素過程と呼ぶことが許されよう。J=1のケースを含めるならば、有限理論の範囲内では、任意の量子過程に対して素過程への分割が行える。J=1のときは、元々の量子過程Ωが素過程である。
各素過程には、(8)式で定義される正数ωkが与えられ、量子過程Ωの遷移確率はωkの和となる。このことより、ωkは素過程Ωkの先験的確率と見なされる。
素過程への分割は、必ずしも一意的でない。このことは、行列Rの非対角要素のほとんどが0で、所々に+1と-1が存在しているという特殊なケースを考えれば、了解されるだろう。ある非対角ブロックにどの+1と-1を入れるかという点で、任意性があるからだ。ただし、現実的な系の作用積分では、何らかの変換操作で結びつけられるような経路同士が打ち消しあうはずであり、それ以外の相殺は、あるとしても偶然的なものでしかない。偶然の相殺が起こらないという条件の下では、一意的に素過程に分割できると推測される。
上で定義された量子論的な素過程は、Griffithsらが導入した「履歴」のアイデアの二番煎じにすぎないが、量子論に対する基本的な態度は異なっている。「履歴」について取り上げる研究者は、一般に、ある時刻tjにおける排他的な事象を射影演算子の集合{Ek(tj)}で表し、Ek(tj),Ek(t2),…,Ek(tn)を継起的に作用させることによって事象の連鎖としての履歴を定義する16)。これは、「事象の生起」という古典論理が適用可能な概念に基づいて、量子力学を解釈しようとする試みだと言える。ただし、事象を定義する射影演算子の選び方には、任意性が残っている。多くの研究者が試みているように、ある物理量のスペクトルが一定の範囲内に落ちる領域へ射影する演算子を選んだ場合は、この物理量の値が不定性を伴いながら刻々と変化していくという“わかりやすい”履歴が描かれるが、その一方で、整合性条件を厳密に成り立たせることは困難になり、どうしても、ごく微小な干渉項が打ち消されずに残ってしまう。言うなれば、わかりやすさの代償として厳密さが犠牲になってしまったのである。
これに対して、著者は、量子過程には二重スリットでの干渉やクーパー対の形成のように日常的な概念によっては理解できないものが多いとの認識から、古典論理の枠内で量子力学を了解しようという試みを端から放棄する。もちろん、古典論理が全く適用できないわけではない。個々の素過程においても、先験的確率を与える経路積分の途中に、特定の事象を表す射影演算子E、または、その排反事象の演算子1-Eを挿入することができる。このとき、いずれか一方の計算結果が相対的にきわめて小さくなったときには、「この事象が生起している」あるいは「生起していない」と合理的に主張される。しかし、多くのケースでこうした不均衡は生じず、各素過程において事象が生起したか否かを明言することは困難となる。
古典論理による了解可能性の代わりに、著者は、整合性条件(7)の厳密さを要請することにより、各素過程Ωkに対して、先験的確率ωkが遺漏なく定義できるようにした。これは、状態関数に現れる確率情報を完全に分離して、素過程による量子論の実体的記述を可能にするためである。
量子力学の確率解釈は、ある始状態から任意の終状態に至るというトリヴィアルな確率１が、特定の終状態に遷移する確率Tfiの和として与えられる（1=ΣfTfi）ことに依拠している。ただし、この遷移確率が量子力学で求められ得る最終的な解答でないことは、継起的に変動が起きる系に量子力学を適用することの有効性が確認されていることから、明らかである17)。そこで、整合性条件を徹底的に適用し、遷移確率の分割(Tfi=Σkωk)を可能な限り押し進めていけば、量子力学から得られる確率情報を絞り尽くせるのではないかというのが、著者の考えである。
この考えが正しければ、素過程Ωkは、ある物理状態についての確率情報を含まない記述に相当するはずである。より明確に言えば、素過程Ωkは、系の物理状態の確定記述を与える。確率情報が関与するのは、Ωkのアンサンブルの中から１つの素過程が実現される場面に限られる18)。具体的には、同じセットアップで繰り返し実験を行った場合、個々の試行において１つの素過程が実現されており、データの統計的分布は、各素過程が持つ先験的確率ωkによって決定される。
素過程Ωkの存在論的な性質は、哲学的に興味深い。ここでは、２つの点だけを指摘しておこう。第１に、素過程は、始状態だけではその後の時間発展が一意的に定まらないという意味で非因果的であるが、始状態から終状態に至る時間的に拡がった全体があらかじめ与えられているという意味では、決定論的である。第２に、量子揺らぎは、アンサンブルにおける統計的な性質ではなく、関数空間内部での状態の拡がりとしてのリアリティを持つ。第２の点は、クーパー対の形成など量子論特有の現象に関して存在論的な言明を行う場合に、特に重要になると予想される。
誤解のないように付け加えて置くが、本稿は、量子力学の観測問題に関して、何らかの主張をなすものではない。閉鎖系を対象としているために、外部から観測されるという状況が想定されていないからである。あくまで、有限自由度・有限状態の量子力学において確率情報の分離が可能なことを示すための論述である。
1) ＢＣＳ理論についての簡単な解説は、中嶋貞雄著『マクロ量子現象 超伝導と超流動』（講談社）などを参照。
2) 例えば、結晶内部における共有電子の振舞いや、配位子場による無機錯体3d軌道の分裂のように、結晶群の対称性や溶液の色彩に関する間接的なデータから系がどのような状態にあるかが予測されるケースでは、直接観測しなくても、状態関数が物理状態を確定的に記述しているように実感される。
3) R.B.Griffiths, Phys.Rev.A 54(1996)2759. R.Omnès, Rev.Mod.Phys. 64(1992)339. M.GellMann and J.B.Hartle, Phys.Rev.D 47(1993)3345. 各論文に掲げられた参考文献も参照のこと。
4) 特に問題がない限り、この空間はヒルベルト空間と見なして良い。ただし、完備性を要求するヒルベルト空間は、物理的現象を記述するには不必要に条件が厳しい。
5) 有限状態の系を仮定しているので、積分ではなく和で表すべきだが、見やすさを考慮して積分表記にした。また、表記上１変数に限っているが、系を記述する全変数の積分を意味していることは当然である。
6) ここでは、経路積分法については素描的な記述にとどめる。詳しい解説は、R.P.ファインマン／A.R.ヒッブス著『ファインマン経路積分と量子力学』（マグロウヒル出版）、M.S.スワンソン著『経路積分法』（吉岡書店）などを参照。
7) 超ひも理論やM理論のようにあらゆる物理現象を記述すると期待される理論の定式化には、経路積分法が用いられることが多い。
8) exp(iS)が変換行列の有限積で置き換えられるという主張は、有限自由度・有限状態という暫定的な理論でのみ許されるものであり、根元的な理論では、よりエレガントな議論が可能になると想像される。
9) 通常の教科書的解説では、あえて状態関数を定義しないことの方が多い。ψ(q)を状態関数と見なす解釈は、形式的にはCramerの"transactional interpretation"と類似している。ただし、解釈を採用するに当たっての物理的な論拠は全く異なっている。J.G.Cramer, Rev.Mod.Phys. 58(1986)647.
10)R.B.Griffiths, J.Stat.Phys. 36(1984)219.
11)もう１つの考え方として、量子力学はあくまで近似的な理論であり、その計算によって「充分に小さい」という結果が得られたならば、現実の世界では「完全に0になる」と解釈することもできる。ただし、この解釈が妥当かどうかの判断は、近似的でない真の理論が見いだされるまで留保される。
12)量子論的な履歴は、複数の排他的な射影演算子の組{Ek(n)}を作用させて作るが、経路を２つのグループに分けるやり方は、射影演算子Eと1-Eだけを考えることに相当する。
13)U.Eichmann et al., Phys.Rev.Lett. 70(1993)2359.
14)二重スリットを用いたヤングの干渉実験で、どちらのスリットを通過したかが判明すれば干渉パターンが消失するという主張は、1927年のソルヴェイ会議の際に、アインシュタインによる量子力学批判に答えてボーアらが展開した。
15)物理的自由度が１辺がプランク長さ程度の時空領域に１個程度であり、各自由度ごとに102程度の状態数があるとすると、１秒間にわたる１原子の遷移過程の総経路数N=10100程度にもなる。
16)射影演算子の与え方は、研究者によって差がある。Griffithsは、古典論理で事象と解釈できる射影演算子を一般的に想定している。Omnèsは、位相空間内部のある領域(cell)に射影する演算子を好んで用いる。GellMann-Hartleは、物理的な散逸過程を通じて古典力学的な振舞いを示すようになる秩序パラメーターの特定領域に射影する演算子を利用する。
17)すでに、１個の分子が示す継起的な変化が実験的に観測されており、量子力学的な計算と結びつけられている。例えば、Th.Baché et al., Nature 373(1995)132 では、特定波長のレーザービーム中に置かれたC30H16分子が、基底状態S0と励起状態S1の間を振動する途中で、準安定な励起状態T1にしばしばトラップされるという継起的変化が、S1およびT1から放出される蛍光を測定することによって調べられている。
18)「実現される」という表現は不適切かもしれないが、「出現する」や「選択される」でもおかしいので、このまま使用する。
©Nobuo YOSHIDA
info@scitech.raindrop.jp