
現行の場の理論では、(クォークやレプトンなど)多くの素粒子の場が独立に存在し、それぞれ時空多様体上で個別に定義される──という形式が採用されている。しかし、素粒子論研究の主流は、より根源的な統一を求める方向をめざしている。近い将来、統一場の理論が完成し、ただ1つの“原物質”──ある研究者の集団は、それは、紐のようなものだと主張する──の複雑な振舞いを通じて、世界の多様性がもたらされていることが明らかにされるかもしれない。
それでは、統一理論が実現された暁に、時空はどのように理解されるのだろうか。
場の自由度が多数ある場合は、各自由度が共通の土台たる4次元時空多様体の上に乗っていると解釈するのが妥当である。局所相互作用の考えに従えば、それぞれ独立に定義される場の変数のうち、同一時空点ないしその近接点に置かれたもの同士だけが作用を及ぼし合うとされるので、場の定義に先立って時空を与え、しかるのちに、時空上に場の変数を配置しながら相互作用するものを決めていくというのが、順当な理論構成と言える。
しかし、重力場を含めて、あらゆる物理的自由度が1つにまとめられるとすると、それぞれ別個に定義される場同士の相互作用を考慮しなくても良いため、統一された単独の自由度と、その自由度が置かれている時空点とを、あえて峻別する必然性はなくなる。言うなれば、統一場そのものが時空を構成しているのである。アインシュタインの一般相対論は、まず入れ物としての絶対空間を考え、その上で、これを流体状のエーテルで満たす──という古典的な理論構成の冗長性を打破し、空間(および時間)そのものを重力場の媒体たる一種のエーテルとして位置づけることに成功したが、実現されるべき統一場の理論では、時空と物質がそれぞれ存在するという冗長性までもが否定されるだろう。
時空を統一場そのものに還元できるような現実的な理論が、すでにできあがっている訳ではない。ウィッテンらが推進している「超ひも理論」でそうした兆候が見られなくもないが、この理論は多くの難点を抱えており、現実を記述する理論として正当化されるとは、とうてい信じがたい。したがって、時空を場に還元することの可能性については、あくまで推測の域を出ない。しかし、われわれが空間の拡がりを認知する契機となる「物体の移動」が、実は、場の励起状態の伝播にすぎず、また、あたかも物質とは無関係に定義できるかと思われる「空間的な距離」も、重力場によって規定されている──などの物理的事実は、時空と場が切り離しがたい関係にあることを示唆する。
現実的な理論の構築は将来に実現されるものと期待しつつ、とりあえずは、時空を場に還元することについての具体的なイメージをつかむために、「おもちゃモデル(toy model)」を提示したい。考察の対象とするのは、格子場の理論である。この理論は、時空をメッシュに切って個々の領域に1つずつ場の自由度を配していくという(かつて、ハイゼンベルグとパウリが実行した)素朴な量子化の理論を拡張したもので、必ずしも現実的ではないが、直観的に理解しやすいという大きなメリットがある。
格子場の理論においては、時空連続体の代わりに離散的な格子上で場の変数が定義される。直観的なイメージとしては、ジャングルジムのようなものを想定していただきたい。現行の場の量子論の基本的な枠組みと考えられているゲージ理論では、ジャングルジムのバーに相当するのが力を媒介するゲージ場の自由度であり、これが、結節点に該当するクォークやレプトンなどの物質場と相互作用している。

素朴なイメージでは、格子は4次元(時間を含まない場合は3次元)の連続的な時空(座標空間)の中に埋め込まれた形で表される。まず(空間的な)拡がりがあり、その中にジャングルジムが置かれているという発想である。もともと、格子場の理論は、紫外発散の困難を取り除くために便宜的に導入されたもので、最終的には連続極限を取らなければならないと解釈する人も多く、格子が埋め込まれている座標空間は、近づけるべき現実の表現と考えても良いのかもしれない。しかし、格子場で実現される現象だけに着目する場合は、格子上で定義されたダイナミクスのみによってあらゆる過程が記述可能になるため、もはや格子を取り囲んでいるはずの4次元時空連続体が言及されることはない。したがって、格子場の理論が誤差範囲内で現実を的確に表現できる有効性を備えているならば、物理的な実体であるかのごとくに座標空間をわざわざ持ち出し、格子をその中に埋め込むという手順をとらなければならない必然性はない。
きわめて簡単なモデルに基づいて、格子を連続的な座標空間に埋め込まなくても良いことを示そう。格子場の理論を厳密に定式化するには、対称性の一種であるゲージ不変性の要求を満たさなければならず、相互作用の表式はかなり煩雑なものになるが、議論の目的とは関係ないので無視する。さらに、ゲージ場も縮約し、物質場の内部自由度も省略することによって、時空と場の関係だけをあらわにしたい。このとき、(連続極限で高階微分や非線型微分が現れないという通常の仮定の下では)作用積分において次の項(自己相互作用を除く)を考えれば充分である:
S = Σ(i,e) g(e) φiφe・i
直観的なイメージに依拠するならば、φi は、格子点iに置かれた場の変数を表すと解釈される。また、eは格子点の位置iに作用する演算子(一般には複数ある)で、 e・i がφiが相互作用を行う相手(相互作用パートナー)の位置を指示することになる。
いくつかの仮定の下では、このような相互作用の形作るネットワークが(離散的な)時空間と同型になり、格子場を包み込むスペースとしての時空を考える必然性がない(格子場の相互作用だけで時空と同型の世界が実現される)ことが示される。ここでは、格子場の局所的な相互作用を与えるだけで、3次元の離散的ユークリッド空間と同型の立方格子が再構成されるという(いささかトリヴィアルな)例を取り上げたい。相互作用項は、上に与えたものをそのまま用いるが、解釈は異なる。すなわち、φの添字iは、格子上の位置ではなく、単に自由度を識別するインデックスと考える。また、演算子eは、φi と相互作用するパートナーが置かれている位置ではなく、パートナーのインデックスを与えるものとする。このとき、eはインデックス空間のジェネレーターとして機能する。ここで、3つの独立なジェネレーター{ex,ey,ezと、その逆演算子{ex-1,…}が存在し、これらが、
交換則 exey=eyex,…
結合則 ex(eyez)=(exey)ez,…
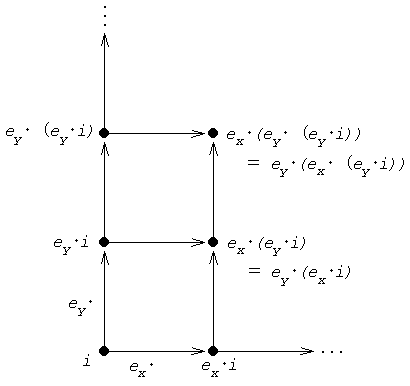
などの線型演算規則を満たしているとする(これは、物理学的には、ラグランジアンで与えられる局所法則の他に、相互作用の形式に非局所的制限を導入することに対応する)。このとき、図に示したように、任意の格子点から出発して逐次ジェネレーターを作用させることによって、あえて座標空間に埋め込むことなしに、立方格子全体を再構成することができる。この格子は、数学的には、{ex,ey,ez}を基底とする整数体上の線型空間の表現と見なされる。
上の議論はトリヴィアルだと思われるかもしれない。しかし、空間的な拡がりが、常にあらかじめ与えておくべき理論の基本的な前提とは限らず、局所的な相互作用の規則から再構成される可能性もある──ということを例示した点は、重要である。この例に従えば、3次元空間+1次元時間の世界があらかじめ存在し、その中で相互作用の形式が規定されるのではない。逆に、与えられた場の変数と相互作用するパートナーの個数として、時空の次元が導出されることになる。
より現実的な定式化においては、重力が本質的な役割を果たすことになると予想される。立方格子の例では、ジェネレーターが線型演算の規則を満たしていることがユークリッド空間を再構成するための条件になったが、少なくとも近似的には一般相対論が成り立っている現実世界では、共変微分の交換関係に現れるアフィン接続の形式を再現する規則を与えなければならない。こうした規則は、線型演算規則のように“ガチガチ”の格子を組み上げるものでなく、アモルファス(不定形)な時空を構成し、回転ような連続変換に対する対称性を近似的に保証してくれるかもしれない。
以上の考察は、強固な論拠を持たない推測の上に成り立っているものだが、それでも、充分に示唆的だと信じる。場の理論を構築する上で、連続的な座標空間をあらかじめ仮定する必然性はない。あるいは、さらに一歩踏み込んで、次のように主張したい:すなわち、物理的世界の基本的な要素/法則とは、可算個の場の変数、これらの間の相互作用の形式、および、相互作用パートナーを指示するジェネレーターの演算規則である。これに対して、時空多様体は、相互作用のネットワークとして派生的に構成されるにすぎない。この立場からすると、虚構的な時空に代わって、場の変数φが張るきわめて高次元の空間に、物理的実在性が認められることになる。
©Nobuo YOSHIDA
info@scitech.raindrop.jp