科学的な理論構成の手法

　歴史的に見ると、科学理論を概念的に構成する手法は２段階にわたって進展してきたことがわかる。すなわち、19世紀中葉から20世紀初頭にかけて整備されたモデル化の手法、および20世紀中葉以降に発展したシステム論的手法である。この２つの手法について、簡単に解説しよう。


モデル化の手法

　はじめに、理念型としての「モデル化された理論」を考察する。ここで謂う所のモデルとは、実体に関する直観ないし哲学的世界観に煩わされずに、一定の要件をインプットしさえすれば必要な結果が求められる機能モジュールを指し、理論を具体的にするために利用される狭義のモデル（神経回路理論のマカロック／ピッツのモデルや大統一理論のＳＵ(5)モデルなど）とは異なる意味を持たせている。このように機能モジュールとしてモデル化された理論は、その概念枠や機能、適用範囲が明確に定められねばならないため、理論を構築する際にはこの要件を満たすための作業が必要となる。以下では、こうした作業を、概念化、理想化、数理化の３つ段階に分けて、その具体的な内容について見ていく。

  1. 概念化　： 　科学理論をモデルとして明確に記述するためには、理論で使われる話用語を外延が指定できるような形で内包的に定義しておくことが望ましい。このような定義の作業を、理論の概念化と呼ぶことにする。
    　当然のことながら、科学的概念は、決して科学全体を厳格に支配するものではなく、多くの不定性を含んでいる。
    1. 科学的概念は、一般に厳密に定義されているのではなく、異なる理論に流用したり理論の発展に応じて変形する余地が残されている。　【例】「遺伝子」の概念は、生物学理論の最上位層では遺伝形質の素因子として緩やかに定義されており、集団遺伝学にも分子遺伝学（「偽遺伝子」も登場する！)にも利用できる。また、「出産時ストレス」のように、異常児の多発性の原因として概念のみを先行して与える場合もある。
    2. 科学的概念はパラダイムの転換に連動して変化していくものであり、学界の共通認識として揺るぎない形で固定されるには長期間を要するのが一般的である。　【例】近代物理学における「質量」の概念は、全ての物体に備わっている示量数に始まり、ラプラス的な世界観の下で各質点に与えられた（マッハによれば未定義の）定数としての地位を獲得したものの、特殊相対論によって運動に依存して変化する量に読み直され、現在では方程式に特定の項に現れる定係数と見なされるに到っている。
    3. 科学的概念を自律的に定義することは、科学の全ての局面にわたって可能なわけではなく、こんにちなお少なからぬ科学的命題が日常的な直観を頼りに語られている。その事例は、相互依存関係がきわめて複雑で還元主義的手法が通用しない対象、なかんづく生理学的システム（免疫応答や学習記憶を司る系など）を取り扱う理論に見いだすことができる。

    　以上の議論から指摘できるように、科学的概念は一般に理論を分節化する際のメルクマールにすぎない。結果的に、方法論としての概念化も、安定した科字理論の確立に直結することはなく、理論を構築する過程での一時的措置にとどまる場合も稀ではない。

    　にもかかわらず、たとえ厳密でも全般的でもないにせよ、諸用語に内包的な定義を与えようとする概念化の作業は、日常的直観から切り離された自律的なモデルとして理論を確立するために必要不可欠であり、さらには、科学的議論が非科学の領域にどこまで通用するかという領域画定の役割をも担っている。このことは、科学的概念に染みっいていた生活世界の残洋が無用な哲学的議論を惹き起こした実例――古くは「潜勢力」としての意味を与えられていたエネルギーに関する概念的混乱から、新しくはアロステリック効果を下敷にした偶然か必然かの論争――を想起すれば理解できるだろう。こうして、概念化に際して最も重要な過程は、理論の構築に有害な生活世界の諸要素をいかに排除するかにあることがわかる。

    　この点を明確にするために、ここでは生物学における「適応」という概念を例として取り上げよう。一般に適応とは、与えられた環境の下でより生存に適した形態、機能または行動の獲得を表す概念であり、その内容がきわめて広範にわたることから、もともと対立する立場であるはずのラマルキズムにもダーウィニズムにも理論を記述するためのキーワードとして同様に採用されている。しかし、引用法がいかに多面的であろうとも、科学的概念としての「適応」は、日常的用語法とは質的に一線を画するものである。実際、日常的な意味で「適応する」とは、与えられた環境に最もふきわしい形態等を獲得していることを指すが、この立場からは、アフリカの大地に適応していた猛獣が動物園の狭い艦に移されて、なおかつ故郷にいるときより長生きできるという事実が説明できない。こうした困難を回避するため、多くの科学理論では、適応形態を環境の一意的関数とせず、特定の条件の下で形態等についてのパラメーターを可能な範囲で変化させたとき種の生存確率が極大になる点と見なしている。この結果、適応とは、決して生物種にとっての最適戦略ではなく、むしろ漸進的な変化の行き詰まり現象として把握することができるのである。観測データによれば遺伝的多型性が意外に豊富（ショウジョウバエで遺伝子座位の約30％）であることから、低い淘汰圧の下で遺伝子浮動による緩やかな進化が実現しているという可能性は高く、上記の適応概念の妥当性を傍証している。

    　如上の議論から読み取れるのは、科学的概念が日常的直観とは別個の論理で定義されており、それゆえにモデル化された理論での議論が可能になっているという科学理論の構造である。しかも、既に述べたように、ここで謂う所のモデルがあくまで特定の範囲でのみ通用する機能モジュールに過ぎないものである以上、科学における諸概念も、過度の一般化を避けて、モデルが機能することを基本日標として定式化されていることは見やすい。
    　もちろん、常にこうした概念化が功を奏する訳ではない。例えば、高度に抽象的な学問である数学において開被覆によって明確に定義されているハウスドルフ多様体を取り扱う場合ですら、数学者が想を練るときに利用するイメージは、しばしばゴム膜のような固有の計量をもつ日常的な素材に依拠している。また、もともと巨大化した理論を整理するためのメルクマールにすぎなかった概念が一人歩きを始めて混乱を生み出すこともあるかもしれない（アメフラシの産卵行動をどごく一部の実例しか知られていないにもかかわらず、「行動の遺伝因子」が論争を生む場合のように）。しかし、こうした問題点はあくまで、ある程度の基盤が作られた学問を遂行する上での例外的なケースであり、概念化が科学理論を構築する第一歩だという基本的構図は変わるべくもない。

  2. 理想化　：

    　科学理論のモデル化を進めるのに必要なステップとして、次に理想化の作業を考察しよう。ここで理想化とは、自然現象の完全な把握を目標とせず記述可能な近似的体系を構想する作業で、理論と現象のずれは摂動として別個の研究対象と見なされる。

    　歴史的に見ると、科学が世界の真の姿を記述しているという信念は17世紀以降の近代物理学の勃興とともに強まリ、19世紀半ばには力学および電磁気学の理論によって原理的には全自然現象の確定的な記述が可能であるという見解も現れた。しかし、量子力学の出現により事態は一変した。ある理論が、自然を直接的に開示するものでないにもかかわらず、完全かつ有効であり得るという認識が生まれたのである。

    　量子力学に関する一般の科学者の理解は、次のようなものである：

    1. 量子力学は、波動関数によって状態の確率振幅を与えるにすぎず、自然そのものに即応した記述ではない。
    2. にもかかわらず、科学理論として量子力学が完全かつ有効である。

    　量子力学の有効性については、現在の物性理論の多々ある業績、特にエレクトロニクス分野での成果を想起すれば納得がいくだろう。一方、理論の完全性とは、無矛盾の公理体系を構築できることの謂いであり、当該理論内部では証明できない仮定、あるいは他の理論から得られる結果を援用する必要がないことを意味する。この点に関しては、既に量子力学の公理化が完成されておリ、その完全性が明確になっていることを指摘しておこう。

    　「現代において最も大きな成果を生みつつある物理学理論が、実は、自然現象そのものの記述ではない」という事実は、物理学が真なる演繹体系であり、理論と観測のずれは単に未知の境界条件に起因するというラプラス的な世界観を揺るがすのに充分である。もちろん、将来の科学革命によって自然の本質を開示する理論が現れないという保証はない。しかし、たとえ現行の理論が暫定的なものにすぎないにしても、各方面に応用する際の有効性を否定することはできないはずである。こうした議論を踏まえて、科学とはあくまで特定の応用のために理想化されたモデルを取り扱う学問であると主張しよう。換言すれば、科学は自然とは何かを語るのではなく、自然に関して「役に立つ」報告を与える手段と言える。

    　こうしたある意味ではプラグマティックな側面は、科学的記述を自然そのものから乖離させる危険を常に李んでいる。生理学を例にとって説明しよう。生物の体組織を対象とする実験には、in vitro（生体外）とin vivo（生体内）の２種類があり、後者の方が確実に自然の実態に近いものである。ところが、生体現象ないくつかのメルクマールによって分節化し相互の影響関係を体系的に記述しようとすると、in vitroで単純化された現象の方が一般に理論に馴染みやすい。例えば、ニワトリの胚から切除した交感神経節をマウスのある種の肉腫細胞の近傍で培養すると腫瘍に面した側に偏った神経繊維のハローが見られるという実験結果から、溶解性の神経成長因子（ＮＧＦ）が神経突起の分化と成長を活性化するという図式的理解が得られ、教科書にもそのように記述されがちである。しかし、こうした理解はあくまでin vitroの現象に限定されるものであって、in vivoでは何重ものフィードバック機構を含むきわめて複雑な調節過程が実現されている。従って、「ＮＧＦ→神経成長」という図式を医学の局面に拡張して応用しようとすると、予期せぬ障害が発生することがあり得る。

    　このような問題を回避するために、現代科学は、その教科書的記述において一般に「但し書」つきの体系化を試みる傾向がある。すなわち、理想化された理論を基幹としながらも現実の自然は常にそこからの差異を含むことを主張し、問題となる差異は新たを研究の対象と見なすのである。この手法は、しばしば科学理論のクラスター化を促進する。先の例を再び用いれぱ、ＮＧＦの生理活性機能と調節機能をそれぞれ独立した領域として別個の研究者が取り上げている現状が、このクラスター化現象に対応している。もちろん、現実の科学が常にこのように効果的な体系化を実現している訳ではない。しかし、研究者が期待するのは、こうした「但し書」の集積によって、科学が漸近的に自然への密着度を高めていくという発展的プロセスである。

  3. 数理化　：

    　モデル的理論を構築するための作業として最後に考察するのは、数理化の技法である。ただし、ここで言う数理化とは、物理学における解析的手法のみならず変換の理論に基づいて離散系を取り扱う手法をも含めて、科学的議論を半自動的に遂行できるような方法論を理論に取リ入れていく過程を指す。

    　まず、数理化の問題を論じるための準備として、科学的議論の形式について考察しよう。一般に、科学理論が具体的に応用される際には、与えられた前提からどのような結論が引き出されるかが問題となる。しかるに、ある理論の守備範囲内での前提の種類は通常きわめて多様（場合によっては無制限）であるため、前提と結論の組を理論内部に羅列的に収録することは不可能であり、何らかの方法で形式的推論を行わなければならない。古典的な論理学では、因果律が形式的推論の枢要な地位を占めているが、科学の世界では事情が異なっている。これは、原因と結果を直接結びつける因果律が中間の過程を省略しているためではない。実際、化学における触媒の説明は、「酸はサッカロースの加水分解を促進する」というように具体的作用の記述を省いていても、科学的に有効である。この点について説明を試みよう。

    　おそらく、こんにち物理学を勉強する学生は、科学哲学で馴染み深い原因と結果という概念が、その教科書から事実上消滅していることに気づくだろう。これは、古典的な原因概念である「動力因」が、きわめて単純なシステム以外では余り有用でないことに起因する。例えば、ポテンシャル関数の極大値に当たる不安定平衡の状態にあった系が微小な揺らぎのために極小値の状態に遷移した場合、この遷移の動力因が揺らぎであることに間違いはないが、より本質的な役割を果しているのは極大値と極小値を持つポテンシャル関数の構造それ自体のはずである。このように系を成立させている構造に帰着させられる原因を「構造因」と呼ぶことにすると、明らかに、現代科学の対象となるようなシステムにおいては、動力因よりも構造因が現象の性質を定める主要因となっている。しかし、科学的記述の中で構造因があからさまに語られることは少ない。なぜなら、構造因の性質から予想されるように、原因の説明はシステムの構造に関する記述に事実に吸収されてしまうからである。さらに、構造因の概念は離散的なシステムにも拡張可能で、この場合は、各要素間のリンクによって構成されるネットワークが構造を与えていると見なされる。こうして、科学において前提から結論に到る論理の流れは、単なる「原因（動力因）→結果」の連鎖ではなく、システムの構造を与えるのに必要な諸要素およぴ要素間の結合関係（＝法則）をもとにした操作的過程であることになる。ここで、法則とは、連続系では方程式を、離散系では変換規則を指すと考えて良いだろう。以上の議論をもとに、数理化とはシステムを要素とその間の関係によって記述する作業を指し、科学における推論形式を明確にするための処置であると主張したい。

    　数理化の内容を、より具体的に考察していこう。ただし、方程式に基づく連続系の理論が数理的なのは明らかなので、ここでは離散的なシステムを対象とする理論を数理化することの具体的意味に議論を限定する。既に述べたように、このような理論ではシステムの構成要素問のリンクを問題としなければならない。この点について、分子生物学を例に説明したい。

    　こんにちなお細胞の分化のメカニズムには多くの謎が残されているものの、分子生物学者は、不明な部分が理論の有効性を損なわない形でこの現象を記述することに成功している。このことは、遺伝子の発現に関する記述に典型的に現れている。20世紀中頃までは、遺伝子の発現とは、遺伝子型と表現型のリンクの形式であった。その後、ＤＮＡの構造と機能が解明されるにつれて、この２つの要素を媒介する中間項として調節タンパクの存在が明らかになり、遺伝子によるタンパク質の合成とタンパク質による遺伝子の調節という新たなリンクが追加されるに到った。最近では、各遺伝子のやや上流に「プロモーター」と呼ばれる領域が存在し、これに活性（抑制）因子であるタンパク質分子が結合するとＤＮＡの転写が開始される（されない）ことが判明している。こうして、次のような基本的な構造と変換規則が得られる：

    1. プロモーターと活性／抑制因子は結合というリンクで結ばれておリ、一方のリンクがオンになると他方は自動的にオフになる。
    2. 活性／抑制因子の結合リンクのオン・オフは、プロモーターと遺伝子の間の（転写の）開始というリンクのオン・オフを支配する。
    3. 遺伝子（ＤＮＡ）とｍＲＮＡの間には転写のリンクがあり、これは転写の開始によってオンになる。
    4. 活性／抑制因子は別の遺伝子と（ｍＲＮＡのノードを介して）リンクされている。

    　以上のような基本図式（もちろん、実際にはこれより遙かに複雑で、ときには量的な扱いが必要になる）に、具体的な遺伝子、プロモーター、活性／抑制因子を代入することにより、分子生物学における形式的推論が遂行されることになる。

    　ここで重要なことは、離散系での変換規則は、その中間に予想される具体的な過程を黙殺しているという点である。実際、プロモーターに活性因子が結合するとＤＮＡの構造変化があって転写の開始に到ると想定されているが、この過程を無視して「活性因子の結合→転写の開始」という単純な図式を与えても理論は有効である。こうして、科学者はいたずらに繁雑な議論に巻き込まれることなく理論を応用することが可能になるのである。

    　なお、上に述べたような数理化によって得られた連続系の方程式ないし離散系の変換規則は、今後は一括して「法則」の名称で呼ぶことにする。

　以上のような作業によって構築されるモデル的理論は、必然的に次のような性質を具備することになる。すなわち、概念化・理想化の結果、モデルとしての理論は自然の実体を直接的に表現するものではなく、あくまで特定の目的に従属した道具として利用されることになる。さらに、数理化によって半自動的な推論が可能になっているため、理論を利用する個人の生活史が関与する余地が少なくなり、得られた結論の（当該理論の前提の下での）普遍性が保証される。こうした性質は、現代科学が技術文明の発展と軌を一にし、技術者の意向に強い影響を受けながら従前の自然哲学的様相から変貌していったことを反映していると考えられる。

　理論をモデル化するという現代科学の方法論は、しかしながら、哲学的に見てある深刻な問題を惹起する。自然の現象の中で数理的な議論によってカバーできる範囲は現時点では必ずしも広いものではなく、従って、哲学的な自然観のように現象全体を包括する理解が必要となる問題にまで論述が及ぶことは、正当な科学論文では稀である。ところが、科学者の側からすれば、研究対象とする理論に含まれている自然の理解法を、より広範な自然認識に拡張したいという欲求はきわめて当然のものである。こうして、科学的方法論によっては正当化され得ない自然観が、まきに科学を遂行する当事者である科学者によって支持されるという奇妙な事態が生じる。例えば、海馬体のシナプスにテタヌス（高頻度刺激）を与えると興奮性シナプス後電位の振幅が長期にわたって増大するという現象が観察されるが、これはあくまで神経細胞レベルでの生理学的な性質にすぎない。ところが、一部の学者はこの現象を学習記憶のモデルと見なし、人間の知的活動が神経レベルの現象に還元できるという（科学では正当化できない）自然観の根拠として利用している。しかも、この自然観は、単に哲学的思索の原点になっているのみならず、テタヌス後の長期増強を高等生物の学習と結びつける目的で、条件づけがなされたウサギの歯状回で貫通繊維の変動電位を測定するという新たな（科学的方法論に則った）実験の実施を促すという科学的帰結をもたらしている。

　このような非・科学的な（しかし有意味な側面を有する）自然観の科学における役割は、科学を動的な体系と見なすことによって初めて明らかになる。実際、科学がその内容を更新していく過程で、従前の理論を逸脱する自然観が新しい発想の淵源になっていることは数多い。ただし、こうした発想は科学的方法論の枠内にはない（従って論文にあらわに記されることは少ない）ため、研究結果の交流（次節で述べる機能バケットの交換）の場で哲学的な自然観が重要な役割を果たすとは考え難い。事実、現代素粒子論の一つの成果である大統一理論は、当初は「自然は単純を好む」という自然観に基づいて構想されたものの、その後の進展においては、いくつかの実験事実（観測される素粒子の質量がきわめて小さいこと、あるいは右巻きニュートリノや磁気単極子が発見されないこと｝との弱合性を保つために、例外群を利用したリ複雑な群表現を導入するなど、統一前と同程度の複雑さを理論に内包するに到っている。これを模式化して言えば、「単純な自然」の観念は、大統一理論の根本的な要素としては他の学者に伝達されなかったのである。この例が端的に示しているように、科学における自然観は、科学の動的な局面において科学者個人の発想を下支えするものではあっても、より重要な理論運営には余り関与しておらず、理論の展開を拘束することはない。しかも、発想の段階においてすら、当の自然観が必須であるという根拠はなく、別の科学者が全く異なる見地から同じ理論を案出する可能性は充分にある。従って、哲学的な自然観が科学内部において果たす役割は科学の構造・機能を論じる上でそれほど大きいなものではなく、少なくとも科学的方法論の議論からはこれを除外してしかるべきである。言うなれぱ、科学者の自然観は、それ全体が科学哲学よりは思弁哲学の問題なのである。


システム論的手法

　前節の議論は、モデル化された科学理論をいかにして構築するかに焦点を絞っていた。次の段階としては、こうして体系として成立した理論をどのように運営するかを考察するのが妥当だろう。

　19世紀後半までの科学者は、専門領域に関してなら基礎から応用まで見渡すことが可能だったと思われる。しかし、現在のように科学の応用範囲が膨大なものになると、職業科学者による特定ジャンルごとの分業化が進んで、科学はそれ自体が複雑な階層を有するレヴィアタン的存在と化し、これを手なずけるために特殊な科学的方法論が要請されるに到った。この傾向は、科学が自己組織化を示すような複雑系を研究対象の中に取り込むにつれて、さらに顕著なものとなってきている。

　それでは、現代科学が採用している手法とはどのような基盤に立っているのだろうか。私は、この思想基盤を「機能主義的システム論」という語で表現したい。ここで、機能主義とは、理論の応用という機能的な側面に重きを置く立場であり、諸現象を概念的に関連づけて解説する「説明カ」よりも、実験データの予測値を半ぱ自動的に生成する「予言能力」を評価基準の中心に据えるものである。また、システム論は、理論の階層化を図る際の指導原理として援用され、階層間の相互作用の形式を決定する役割を果たしている。以下では、こうした手法によって現代科学がどのように運営されているかを、具体例を交えながら見ていくことにしよう。

　本論に入る前に、上の解説で用いられたいくつかの用語を明確にしておく。

　以上の基本的用語法を踏まえた上で、次に、科学理論の運営法についての議論に移ることにしよう。

  1. 理論が機能する環境

    　はじめに、理論が機能する環境について考える。

    　古典的な科学理論では、そこに現れる諸用語は対応する実体との関係で記述されることが一般的だったと思われるが、現在では、理論の基盤となる基本的な概念や法則の多くは、当該理論を道具として使用する科学者の間での暗黙の了解に任されている。こうした了解は階層的であリ、その最下層は人間に共通な認知の方略に依存しているため、説明的記述が困難である。しかし、理論運営の実用上は研究方法の異なる理論との関係を考慮すれば充分なので、各理論間の差異が明らかになる範囲で基本前提が明文化されていると仮定する（「遺伝子は染色体上に特定の座位をもつ分割不可能な単位とする」あるいは「場の演算子のフーリエ成分は素粒子の生成・消滅演算子を表す」のように）。

    　ここで重要なのは、こうした基本前提は、理論を完全に拘束するものではないという点である。このことは、理論物理学のような演緯的な学問にも該当する。例えば、場の理論では、時空は４次元ミンコフスキ多様体であると前提されているが、個々の理論の中には、格子ゲージ理論のように時空点を離散化するものや超対称性理論のように時空を４次元以上に拡張するものがある。しかし、こうした理論が従来の枠組みから根本的に逸脱した革新的主張かというと決してそうではなく、単に、前提となる基本概念に、「近似的にそのように観測される」という但し書を付け加えたに過ぎない（前節の概念化および理想化の項参照）。従って、ここで謂う所の基本前提とは、理論に含意されている概念・法則の理想化された形式と言っても良い。

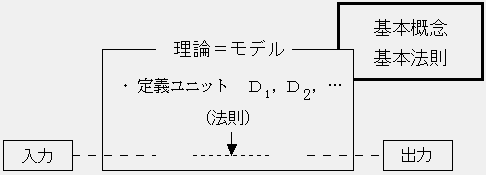
    　一般に、理論（＝モデル）の定義では、援用される概念・法則が個別的に列挙されているので、各々の条項を簡単に定義ユニットと呼ぶことにしよう。定義ユニットは概念・法則の記述であるが、必ずしも自己完結的ではなく、他の理論の内容を引用することも多い。しかし、その場合でも、引用するのは理論の全体ではなく、ある限定された機能であるため、ユニット的な性格は変わらない。

    　以上のようにして定義される理論に適当なデータ（観測された、または仮説的な）を入力すれば、理論の法則に則ってある理論的命題が出力される。こうした状況を模式的に表すと、次のようになる：

    sub01_01.gif

  2. クラスターの構造

    　次に、理論運営の基本単位を明らかにするために、現代科学における理論間構造（いくつかの理論が集合して形成する構造）の特徴を考察する。

    　現代科学の諸理論は、ある理論での定義ユニットが別の理論の基本前提をなすという形で錯綜した構造を形成しているが、その中にあって、ある種の秩序を指摘することできる。それは、一定の機能をもつ理論の集まりが階層的にクラスター化されているという際だった特徴である。このクラスターの概念について若干の説明を試みたい。

    　はじめに断わっておくが、クラスターは決して独立した存在として定義されるものではなく、その境界も結晶の界面のように明瞭に定まってはいない。科学理論が織りなす構造の微視的なイメージは、むしろアモルファス状態に近いものがある。アモルファス状態では、ある原子に着目するとその近傍の原子は整然と並んでいるように見えるが、そこから遠ざかるにつれて秩序が失われ乱雑さが顕著になる。これと同様に、研究領域がオーヴァーラップする理論は使用するテクニックや論理の組み立てが類似していることが多いが、領域が離れるにつれてはっきりとした差異が目だつようになる。しかし、科学の現状を適当に粗視化すると、他と比較して共通の目的意識を有している理論の集合が浮かび上がってくる。具体的には、現存する学会の分科会がこれに対応すると考えて良いだろう。このような集合を称して、ここでは便宜的にクラスターと呼ぶことにする。

    　筆者が想定するクラスターの概念を明確にするために、クラスターの構造および機能に関する特徴をそれぞれさらに２点ずつ指摘しておこう。

  3. バケットの交換

    　上に述べてきたクラスターの概念は、単独では余り有用なものではない（科学はいくつもの分野をもつという当り前の主張に過ぎない）。これが意味を持つのは、次に論じるバケットの概念を援用する場合である。

    　科学論文が他の方法論による有効な記述と叙述の形式において際だって異なっているのは、前者が、理論内部で頻繁に理論的命題を生成して提示するという点である。電気機器の取り扱いマニュアルや情報収集企業の報告書では、命題は一般に提示されるだけで理論的に生成されるものではない。また、人文科学の著作では、議論の展開に多くのスペースが費やされて、命題が提示される頻度は科学論文に比べて少ない。さらに、科学論文の場合、他の論文からの引用がきわめて多いのも特徴である。

    　こうした叙述形式は、科学における理論運営の特色を反映するものと考えられる。この点を、以下に説明しよう。

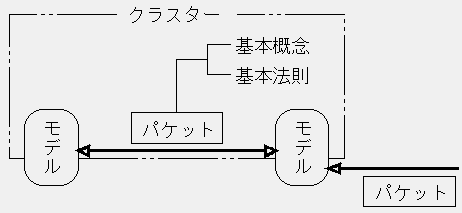
    　科学論文における命題提示や引用の多さは、科学がさまざまな研究成果の交流を通じて発展するという運営上の特色を反映するものだが、その具体的方法には、科学に固有の性質が見いだされる。すなわち、理論内部または理論相互間で交換される内容は、小さな単位に分割された独立の命題の形式をとる。こうした命題は、日常的用語で語られることはなく、特定の理論に即した諸概念・法則の枠内で提出される。従って、交換されるのは、「命題」と「命題を解釈するための概念・法則」をセットにしたものとなる。いわば使用説明書つきの道具であるこのセットを、「機能バケット」、あるいは単に「バケット」と呼ぼう。バケットが同一理論内部で交換される場合は、バケットにおける解釈の前提は当該理論の定義ユニット（および基本前提）である。また、バケットの交換が異なる理論にわたるときは、理論を包含するクラスターの基本概念・法則がバケットにおける解釈の前提となる。従って、いずれの場合も、バケット自体にはその解釈法が書き込まれてはいないが、その所属が明らかである限り、これを実際に使用する科学者が意味を取り違えることは稀にしか起こらない。以上を模式化すれば、次のように表されるだろう：

    sub01_02.gif

    　科学理論の運営においてバケットの利用が有益なのは、情報を交換するとき理論全体に言及せずに特定の機能だけを伝達できるからである。もし私が、体系的認識のセマンティックな構造を調べるために日常的レベルでのシンタクティックな操作を中止することを《エポケー》と呼んだとすると、現象学の専門家から概念の誤用を厳しく指弾されることだろう。哲学的な用語は、一般に、その概念を採用している学問体系全体の一貫性から逆に規定されるのである。これに対して、科学的命題は、理論内部での機能さえ保っていれば特定の学説に束縛されることはない。例えば、ミトコンドリアＤＮＡの変異が分子時計として利用できるという結果が提出されれば、どの進化学説を支持するかにかかわらず、現在のＤＮＡの塩基配列データからヒトと類人猿の系統樹を推定することが可能である。このように、さまざまな理論から結果を流用できることが、科学理論の運営における大きな特色となっている。

    　バケットの利用は、各理論の自律性を最大限に尊重するものである。既に述べたように、科学における理論間構造は自然界の階層性を直接に反映しているのではなく、自然の階層で上位に相当する理論が下位の理論を拘束することもない。実際に行われているのは、各階層間でのバケットによる情報交換であり、これを除けばそれぞれの理論が事実上独立に機能しているのである。このことは、地球物理学と地震学のような実例を想起すれば理解できるだろう。

    　以上のように、「バケット」は科学の実態を解説するのに便利な概念ではあるが、バケットを厳密に定義することは困難であるのみならず、おそらくは無意味である。なぜなら、現実の科学的活動で交換される命題は、小は単純な数値データから大は特定の理論の機能全般に関わるものまであり、概念画定するための適当な単位が存在しないからである。実際、理論物理学で数学の技法を援用する場合、集合や演算の定義の詳細には拘泥せずに応用数学の教科書に掲げられている「定理」を利用する（「コンパクト性」は有限の拡がりを指すという程度の理解で方程式系における解の存在定理を主張するように）という点で機能的な引用であることは間違いないが、その内容の広範さを考えれぱ「バケット」という名称はふさわしくないように思われる。しかし、これは単に命名法の問題であリ、これ以上議論する必要性は感じられない。

    　ここまでの議論では、主としてバケットを用いることのメリットを見てきた。しかし、機能的なバケットの受け渡しが、常に妥当な結果を生むとは限らない。この点について、科学論からはやや離れるが、身近な例で考えよう。大規模建築物の耐震性を解析する場合は、数例の典型的な地震波をコンピューターに格子近似で入力し、各点に加わる応力をシミュレートして建築資材の耐久性と比較するという手法がとられている。ここでは、地震波のパターンや離散化する際の近似法などに、他の学問分野からモジュール的な知識が提供されている。ところが、このような知識が集められれば地震の影響が完全に判明するかと言えば、そうとは限らない。なぜなら、建築物と共震するような「典型的」でない、あるいは、きわめて長周期または短周期で有限の格子近似では再現できない地震に襲われることもあり得るからである。また、工事の手抜きなどにより各部分で所期の強度が達成されていないかもしれない。この例が示しているのは、各バケットは有効な知識を与えるものであっても、それを集積する場の状況によっては妥当な結論が導かれない可能性があるという事実である。科学の体系の中に、このような例が現に存在するかどうか、筆者には不明であるが、現代科学の方法論にある種の限界が存することは心に銘記しておかなければなるまい。


  4. 理論運営の実際

    　最後に、これまでの議論を総合して、科学理論が実際にどのように運営されているかを述べたい。

    　上に（実証的な議論は抜きで）示したように、それぞれの科学理論は、一般にあらわには表記されない基本前提の下で、与えられた定義ユニットに従って自律的に機能しながら理論的命題を生成し、これをバケットの形で他の理論と交換している。こうした過程である理論が妥当でないと評価された場合にどのように取り扱われるかが、科学哲学の観点から特に興味あるところである。

    　いわゆる通常科学の範囲では、理論の妥当性が問題になった場合は、その定義ユニットの点検が行われる。具体的には、いくつかの定義ユニットの修正・追加ないし削除によって、理論が有効に機能するようになるかを調べることになる。近年に見られた免疫学の展開は、こうした作業の典型例を提供してくれる。初期の理論では、免疫応答の調節機構が充分に理解できないまま、リンパ球を形態からＢ細胞・Ｔ細胞に分類して後者に何らかの認識機構が備わっているという漠とした前提を立てて議論を行っていたが、その後の発展では、この（定義ユニットを構成する）諸前提の修正と精緻化が推進されることになる。まず、体液性免疫と細胞性免疫の区別をもとに、Ｔ細胞をヘルパーＴ細胞・キラーＴ細胞などいくつかの種類に分類し、また、単なる貪食細胞と思われていたマクロファージに抗原提示の機能を付与した。さらに、Ｔ細胞が同じ生体の細胞（＝“自己”）を識別するという半ば目的論的な記述を、ＭＨＣ産物との結合という分子レベルでの明確な現象に置き換えている。ここに見られるような定義ユニットの修正は、理論が発展していく場合には常に観察される現象である。

    　このような定義ユニットの交換による理論の変更は、前提となる基本概念や法則の訂正が迫られる場合には、通用しない。ここで必要になるのが、こうした基本前提の書き換え、すなわち、いわゆるパラダイムの転換である。ただし、現代科学においては、こうしたパラダイムの転換は稀であり、従前の基本概念に単なる但し書を付け加えて済ます場合が多い。その典型的な例は、分子遺伝学における遺伝子像が、近年の概念事実の蓄積にともをって、従来の静的なものから不等交叉やドメインの転移によりダイナミックに変化するものへと変更されながら、決して世界観の変革に通じるような巨大なパラダイム転換をもたらさなかったことに見いだされるだろう。古典的な方法論では概念枠そのものの変更を余儀なくされるこうした状況に対しても、現代科学では、単に遺伝子の概念枠の中にある安定性の項目に「統計的に」という但し書を加えれば充分なのである。

    　もちろん、ときとして、現実にパラダイムの転換が惹起される場合もある。近年では、素粒子物理学においてこうした「事件」が起きている。すなわち、1960年代には、相互作用をプラックポックスと見なし散乱行列の解析性をもとに理論を構成する解析的Ｓ行列の手法が広く行われていたが、この手法は70代に入ってからは急速に衰退し、代わって、相互作用をラグランジアンを使って具体的に書き下す方式が全盛をきわめている。このパラダイム転換は、見方によれば、物理学の基本法則が人間にとって未知のものではなくあらわに表記できるという哲学的な意味をもっている。しかし、実際には、そうした問題についての哲学的論争は（ほとんど）見られないまま、それぞれの手法を利用していた学派の盛衰という形でパラダイムの転換が成し遂げられたのである。その理由は、Ｓ行列やラグランジアンのような基本的手法を共有する理論クラスターの存在が、研究者集団としての学派を通じて比較的明瞭に意識されていたため、哲学的な視座を導入することなく「役に立つ」クラスターに乗り換えるだけでパラダイム転換が可能になったためと考えられる。

　以上の議論から明らかなように、現代科学は、理論体系として容易に覆されない高度な安定性を備えており、たとえパラダイムの転換が起きるとしても、周囲ヘの影響が最小になるような「静かな革命」に終ることは必至である。こうした特質は、科学を機能的な道具として利用する社会的要求に合致するものである。



【項目リストに戻る】
【表紙に戻る】

©Nobuo YOSHIDA
info@scitech.raindrop.jp