科学の回廊

アインシュタイン／ボーア論争の勝者

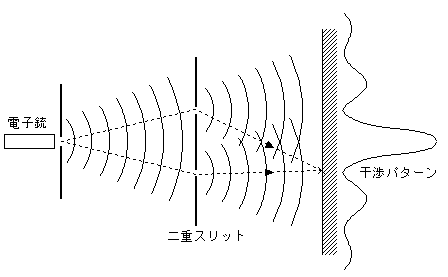
（この小論は、読者が量子力学について理工学部２回生程度の知識を持っていることを前提として、執筆されています）

　量子力学の解釈を巡って繰り広げられたアインシュタインとボーアの論争は、20世紀前半の科学史を飾る象徴的な出来事として有名である。
　すでに相対論の提唱者として高い名声を博していたアインシュタインが、新興理論である量子力学に対して数多くの鋭い批判を提出し、一方のボーア陣営が、こられをことごとく跳ね返して、量子力学の正当性を証明した──論争の顛末は、しばしばこのように紹介される。しかし、アインシュタインが量子力学のどの点を問題ありとしたのか、ボーアらの反論は果たして物理学的に妥当なものだったかについて、科学史家は必ずしも明快に解説していない。歴史的には、1927年（第５回ソルヴェイ会議）から1935年（ＥＰＲ論文とそれに対するボーアの反論）に及ぶこの論争と平行して、量子力学が学界で受容され、多くの重要な応用が見いだされた。しかし、こうした理論的発展は、２人の大家（アインシュタイン、ボーアとも40歳代後半から50歳代）による論争とは無関係に、20～30代の若手・中堅学者を中心に成し遂げられたものである。量子力学が正当な理論としての地位を勝ち得たからといって、論争もアインシュタインの敗北、ボーア陣営の勝利に終わった見なすべきではないのだ。

アインシュタインと量子力学
　そもそもアインシュタインは、量子力学的な発想に闇雲に反対していたわけではない。彼自身、光量子論の提唱者の一人であり、その研究を通じて、光が、波動的であると同時に粒子的に振舞うことを明らかにしていた。彼が望んだのは、原理的に波動性しか示し得ないマクスウェル理論を超克して、波動性と粒子性を併せ持つ根本的な理論を建設することである。シュレディンガーが1926年に波動力学を提唱し、波動場が固有状態を形成することによって（粒子的振舞いを含む）さまざまな現象を生起すると示唆したとき、アインシュタインがこれを支持する立場に回ったのも、この理論が、粒子と波動の二重性という量子論特有の性質がなぜ派生するかを解明する「完全な」理論になると期待されたからだろう。
　しかし、現実の物理学の展開は、アインシュタインが望んだ方向にはなされなかった。シュレディンガーが用いた電子の波動関数は、間もなく電子そのものを表すのではないと判明、1926年のボルンの主張に基づいて、ある場所に電子が存在する確率を表す「確率振幅」であると解釈されるようになった^(*)。分布関数を使ってブラウン運動の解析を行うなど統計力学の分野で優れた業績を上げていたアインシュタインの目に、確率振幅と解釈し直された波動関数は、現象の背後にある微視的な確率過程を粗視化したものと映ったに相違ない。しかし、量子力学の建設者たちは、そうした根源的な実体を解明する努力を怠り、現象論的な議論に終始した（ようにアインシュタインには見えた）。あまつさえ、古典的には解釈不能に見える量子力学の独特の性質に対して、晦渋な哲学的根拠付けを試みることまで始めたのである。その代表例が、ボーアによる相補性原理の主張である。

(*)厳密に言えば、確率振幅には、確率のほかに波動的な振舞いの元になる位相情報も伝えているのだが、ここでは詳細は省略する。

　ボーアの相補性原理は、外見上、粒子の位置や法則の因果性といった古典的諸概念を無批判に適用すべきではないという点で、異なる座標系での同時性や速度の相加性の適用限界を主張する相対性原理と、類縁関係にあるように思われるかもしれない。しかし、この２つの原理は、拠って立つ精神において、本質的に相反するものである。1905年に相対性原理を主張する際に、アインシュタインは、絶対的な同時性を否定し、離れた観測者同士で時計を同期させる方法を操作主義的に定義するところから始めた。しかし、ひとたび互いに運動する観測者と結びついた座標系の変換則が導かれると、この変換則に従う絶対的な座標系を使った演繹的な議論を展開するようになる。アインシュタインにとって、概念の適用限界を検討することは、あくまでヒューリスティックな方法論の一部であり、最終的には、古典的概念を特殊な近似として包摂する一般的な理論を構築することが目標なのだ。これに対して、ボーアは、量子力学においては一貫したロジックを持つ理論の構築を諦め、互いに矛盾するような概念が理論中に併存することもやむなしとする。「粒子性」と「波動性」といった量子力学独特の二重性は、人間の認識能力の限界によって生じる不可避の特性であり、それぞれの概念装置を用いた記述が互いに補い合うことによって、はじめて全体を明らかにすることができるというのだ。このように、物理学の領域に哲学的な不可知論を持ち込むことは、とうていアインシュタインの容認できるところではあるまい。
　ボーアとの論争において、アインシュタインが批判の矛先を向けたのは、量子力学における記述の不完全さである。不確定性関係や非因果性は、こうした不完全な理論がもたらす見かけの性質であり、その意味を哲学的に根拠付けねばならないような原理的なものではない──これが、彼の最も言いたかったことではないかと推測される。
　もっとも、自分で認めているように、アインシュタインは、量子力学を本格的に勉強したわけではなく、これに代わる「完全な」理論を対案として提出できる状況にはなかった。その批判も、原理的ではあっても応用面にはほとんど影響のないものに限られており、形式論争としての性格が色濃い。パウリやハイゼンベルグのような若手の研究者が論争に深く関わろうとせず、量子力学の哲学について熟考していたボーアが過剰なまでに反応したのは、当然のことかもしれない（ちなみに、当時最も深く量子力学を理解していたと目されるパウリは、残された記録からすると、相補性原理をほとんど理解していなかったようである）。

アインシュタイン／ボーア論争
　アインシュタイン／ボーア論争に関して、同時代の第三者による記録はほとんどない。こんにち入手可能な最も信頼できる文献は、ボーアが1949年に執筆した「原子物理学における認識論上の諸問題をめぐるアインシュタインとの論争」（『ニールス・ボーア論文集１　因果性と相補性』（山本義隆編訳、岩波文庫）に収録）であり、これを参考に論争の内容を紹介する。
　論争は、３つのラウンドから成る。このうち、第５回と第６回のソルヴェイ会議の際に戦わされた論争について、アインシュタインが提出した批判と、それに対するボーアの反論を、簡単に表にまとめ、論争の物理学的な意義についてコメントしたい。

第５回ソルヴェイ会議(1927)

アインシュタイン	ボーア
拡がりを持った波動関数は、電子の運動を完全に記述するものではない。二重スリットによる電子の干渉実験においても、電子がスリットを通過するときの運動量移動を測定すれば、電子がどちらのスリットを通過したかがわかる。	スリットを通過するときの運動量移動を測定すると、スリットの位置に不確定性が生じて干渉現象は消滅する。干渉縞を観測し、かつ、それぞれの電子が通過したスリットを特定することは不可能である。

　このときのやり取りは、３回の論争の中でも物理学的に最も有意義であり、1990年代に至るまで、量子力学の基礎に関する研究に指針を与えてきた。
　二重スリットを通過した電子線がスクリーン上に干渉縞を作ることは、量子力学の初等的な教科書にも記されている（下図）。それによると、電子がスクリーンのどの位置に到達したかは蛍光を測定することによって明らかになるが、干渉縞を作るという「波動性」が表に現れている限りは、一方のスリットを通る軌道を描くという「粒子性」は抑制されており、二重スリットのどちらを通ったかを明らかにすることは不可能だとされる。

　アインシュタインは、この不可知性に対して反論を試みた。通常の量子力学の計算では、スリットの存在は境界条件の形で与えられており、電子との相互作用が明示的に示されていない。彼は、この情報の欠如が、波動関数による不完全な記述をもたらしたと考え、スリット板の力学的振舞いを考慮すれば、より完全な──すなわち、電子がどちらのスリットを通過したかを含む──記述が得られると主張した。具体的には、電子がスリット板に与える運動量を測定することにより、電子の回折角を割り出すことができるので、どちらのスリットを通過したかが判明すると考えたのだ。
　ここで注意していただきたいのは、アインシュタインがこの議論で不確定性関係を反証しようと試みたのではないという点である。エーレンフェスト（彼は、ボーアとアインシュタインの共通の友人として、二人の論争に耳を傾けていた）が「（アインシュタインの提出した反例は）ある意味では、不確定性関係をうちやぶるための第二種永久機関のようなものだった」（ホウトスミット、ユーレンベック、ディーケに宛てた1927年11月3日付の手紙）^(*)と書いたこともあって、このときのアインシュタインは不確定性関係を槍玉に挙げたかのように解釈されることがある。しかし、物理的な内容をきちんと理解すれば、彼が常に量子力学の不完全性を問題にしていたことがわかるはずである。エーレンフェストは、「不確定性関係の適用範囲は限られているのではないか」と問題提起したアインシュタインからの手紙（1926年2月12日付）のことが念頭にあって、早とちりしたのかもしれない。実際、この論争の重要な参加者の一人であるパウリは、このときアインシュタインが、波動力学の論理的無矛盾性を承認したものの理論としての不完全さを主張し、「たとえ経験的にもまた論理的にも正しいにせよ、深いところでそれは間違っている」と述べたことを伝えている^(**)。

(*)西尾成子著『現代物理学の父　ニールス・ボーア』（中公新書）p.155
(**)ウォルフガング・パウリ著『物理と認識』（講談社）p.222

　アインシュタインの論点は、従来の計算に取り入れられていない相互作用を正しく評価することによって、波動関数のリダンダンシーを縮約できるのではないかというものである。これは、電子のような物質粒子の軌道（位置と運動量）を完全に跡づけようとする旧弊な主張ではなく、統計法則が必然的に抱え込んでいる「わからない前提の混合」──古典的な統計法則において、ある事態が実現する確率は、前提Ａ（Ｂ…）が成り立っているときの条件付き確率Ｐ_a（Ｐ_b…）等々に分解して扱えるはずだが、どの前提が成立しているかわからないときは、それぞれの条件付き確率に前提が実現する確率を掛けて足しあわせたものを使わざるを得ない──を分析的に解きほぐしていこうとする発想に基づいている。
　この思考実験を提出する前に、彼は、スリットを通過して球面波として拡がった波動関数が、スクリーン上に電子が到達したことを表す輝点が現れた瞬間に「収縮する」ことを指摘している。実は、観測した瞬間に収縮する関数は、アインシュタインにとって馴染み深いものである。ドイツ化学熱力学の伝統の中で教育を受けていた彼は、若い頃から統計的な運動の計算に習熟しており、中でもブラウン運動に関しては卓越したエキスパートであった。1906年の「ブラウン運動の理論」という論文（Ann.der Phys.,19(1906)371-）では、調和ポテンシャルが作用する１粒子が周囲の気体分子と相互作用するときの確率分布関数が取り上げられている。統計法則に従う多数の粒子の分布関数とは異なって、１粒子の分布関数は、拡散方程式に従って時間とともに拡がっていくが、「実際の」位置が与えられれば、その瞬間に１点に収縮する。通常はシュレディンガー方程式に従うが観測された瞬間に収縮するという波動関数の振舞いを見たとき、それが以前に自分が研究した確率分布関数と同種のものだと考えるのは無理からぬことである。しかも、アインシュタインは、気体分子と相互作用する粒子の物理的な運動を調べることによって、確率分布関数や拡散方程式をひねり回している限りは決して到達できないいくつかの重要な結論（拡散係数と粒子移動度についてのアインシュタインの関係式など）を導き出せた体験を持っている。波動関数やシュレディンガー方程式の段階にとどまらず、その背後にある物理法則を研究することの重要性を強調したのは当然だろう。
　シュレディンガー方程式に従う波動関数のリダンダンシーを取り除く上で重要だと考えられたのが、他の物体との相互作用である。拡がった波動関数は、電子とスクリーンが相互作用した瞬間に収縮する。あるいは、ウィルソンの霧箱の中を運動する電子は、過飽和状態にある気体分子と相互作用する度に点々と飛跡を残していく（1927年にハイゼンベルグから原子レベルでは軌道という概念は適用できないのではないかと問われて、アインシュタインは、直ちに霧箱の例を持ち出して反論している）。こうした例からわかるように、他の物体との相互作用を理論に正しく取り込むことができれば、無限定に拡がってしまう波動関数を、より現実的なものに置き換えられると期待される。二重スリットによる電子線回折の場合は、スリットと電子の相互作用が正しく取り込まれていないため、二つのスリットをともに通り抜けるような波動関数しか得られなかったのではないか。運動量のやり取りを評価することにより、電子がどちらのスリットを通過したかは判明するはずだ──これが、アインシュタインの主張である。

　これに対するボーアの反論は、初等量子力学の教科書に採録しても良いほど模範的なものだ。電子ビームの波数をσ、それぞれのスリットから１次の明線方向へ回折するときの回折角の差をωとする。この方向に回折されるときにスリット板が受ける運動量は、どちらのスリットを通るかによってｈσωだけ異なる。また、中心軸から１次の明線までの距離は、1/σωになる（下図参照）。ところが、スリット板といえども量子力学に従っている以上、その力学的振舞いは不確定性関係の制約を受けるはずである。ここで、スリット板の（ビームに垂直な方向の）位置の不確定性をΔｘ、運動量の不確定性をΔｐとしよう。明確な干渉縞が形成される条件は、位置の不確定性が明線の間隔より十分に小さいこと（Δｘ≪1/σω）であり、また、運動量の測定によってどちらのスリットを通過したかを弁別するための条件は、運動量の不確定性が反跳運動量の差より十分に小さいこと（Δｐ≪ｈσω）であるが、不確定性関係（Δｘ・Δｐ～ｈ）より、この２つの不等式が同時に満たされることはない。従って、明確な干渉縞が形成されているときに、どちらのスリットを通過したかは判定できないのである。

　ボーアの議論には、後の論者によって、いくつかの拡張が施された。例えば、電子とスリットがやり取りする運動量の大きさを制御できるような装置を設定した場合、この値が小さいときには干渉縞が明瞭だが、大きくするに従ってしだいにぼやけていくことが示される（...Science ...）。すなわち、「粒子性」と「波動性」は完全に排他的な関係にあるのではなく、１つの現象を、文字通り相補的に説明する描像なのである。こうしたマイナーな付け足しはあるものの、反跳運動量の測定に関する限り、ボーアの主張の正当性は広く認められている。アインシュタイン自身もこの反論を受け入れたようで、これ以降は、「電子は二重スリットの一方を通過するはずだ」といった安直な批判は避けるようになる。
　ただし、だからと言って、アインシュタインの批判がもはや完全に時代遅れのものになったかというと、必ずしもそうではない。確かに、電子線回折が生じるような条件の下では、電子がどちらか一方のスリットを通過したと主張することはできない。それは、コヒーレント（可干渉）という前提に反する。しかし、相互作用を取り込むことによって（コヒーレンスを保つ範囲で）波動関数のリダンダンシーを除くという作業は、常に可能である。そもそも、彼の批判は、多くの相互作用を捨象した非現実的なセットアップを仮定することが量子力学の不完全性の起源となっているという考えに立脚するもので、それまで無視していた要素を考察に含めようとするたびに、その有効性を取り戻す。実際、二重スリットの実験に関して、電子の代わりに高エネルギー状態に励起された原子を用い、スリット板の反跳運動量の代わりに通り道に置かれた共振器内部で放射された光子を測定することによって、どちらのスリットを通ったかを確定する仮想実験が提案されたことがある（M.O.Scully et.at, Nature 351(1991)111)。これは、非相対論的な量子力学では考慮されていない輻射場の影響を、新たに議論の対象にするものである。興味深いことに、このセットアップでは、位置と運動量の不確定性による制約がないにもかかわらず、通過したスリットを特定すると、原子の状態がデコヒーレントになって干渉縞が消失することが示された。この結果は、量子力学における粒子と波動の二重性が、位置と運動量の不確定性よりも根源的な特性であることを物語る。アインシュタインとボーアの論争は、仮想的に、物理学者の脳裏で今なお継続中であると考えても良いだろう。

第６回ソルヴェイ会議(1930)

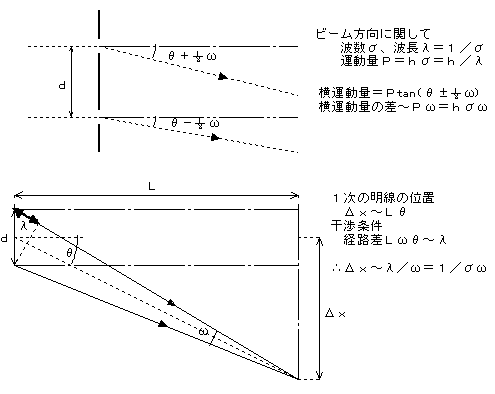
アインシュタイン

ボーア

エネルギーと時間の間の相反的な不確定性は、原理的なものではない。時計と連動しているシャッターの附いた光子箱を用意し、ある時刻にシャッターを開けて光子を放出させ、その前後の質量（相対性理論によれば、エネルギー／ｃ²に等しい）の変化を測定すれば、光子が放出された時刻と、その光子が有するエネルギーが同時に判明する。

一定の運動量を持つ光子を放出すると光子箱の位置が不確定になる。光子箱が重力場の中に置かれている場合、この位置の不確定性によって、質量を測定するための重量秤と、重力ポテンシャルによって進み方が変化する時計の示す値が共に不確定になり、エネルギーと時間の間の不確定性関係が満たされる。

　時間とエネルギーの間に原理的な不確定性がないことを示すアインシュタインの巧妙な思考実験の有効性を、ボーアが一般相対論を援用して論駁した第６回ソルヴェイ会議でのやり取りは、二人の用いた論法がきわめて創意に富み、意表を突いたものだったこともあって、しばしば、両者の論争の白眉と目されている。しかし、詳細に調べると、アインシュタインが、相手方の主張に内在する基本的な欠陥を明確に指摘しているのに対して、ボーアの反論はいささか場当たり的で、物理学的な正当性に欠けるように思われる。

　アインシュタインが時間－エネルギーの不確定性関係を議論の標的にしたのは、きわめて理に叶っている。
　位置－運動量の不確定性関係は、電子のような量子論的物体が点状の自立的な粒子ではないと考えれば、納得することはできる。仮に、電子が電磁場のソリトン解（非線形効果によって生じる孤立した波）のような拡がった存在だとすると、正確な位置を特定することは困難になる。さらに、場の揺らぎの影響で軌道がフラクタル的になるとすれば、位置と運動量の不確定さに相関が生じることもあり得る。位置と運動量の間の不確定性関係は、量子力学が“現象論的な”理論に過ぎないための見かけの性質であり、より実在的な理論を構築することによって、その機序が完全に解明されるべきものである──アインシュタインがそう考えたとしても、不思議ではないだろう。
　これに対して、時間とエネルギーの間に原理的な不確定性関係があると想定するのは難しい。「物体がある位置に存在する」という命題が排他的である（すなわち、それ以外の位置には存在しないことが含意される）のに対して、「ある時刻に存在する」という命題はそうでないからである。別の言い方をすれば、空間的な「位置」が力学的変数であるのに対して、「時間」は単なる座標軸にすぎないのだ。もし、時間－エネルギーの不確定性関係が成り立っていないことを示せたならば、相対論的な不変性を満たさない位置－運動量の不確定性が現象論的な関係式であることは自ずと明らかであり、これに依拠している量子力学が不完全な理論であると結論されるはずである。アインシュタインは、単に不確定性関係を反証しようとしたのではなく、その原理性を否定することによって量子力学の不完全性を証明しようとしたのである。

　一方、ボーアは、空間と時間、運動量とエネルギーの間の相対論的な（４元ベクトルとしての）つながりを根拠に、時間ｔとエネルギーＥの間にも、不確定性関係：
　　Δｔ・ΔＥ～ｈ
が存在しなければならないと考えていた。ボーアにとって、この関係式の成立は、量子力学を体系化する上で欠かせない要件である。実際、彼は「量子力学によって導入されたこれらの新しい原理（＝諸物体の不確定性関係）は、たがいに独立であるのか否か、一方が他方の上位にあるのか、それらは互いに矛盾しているのか、それとも調停可能なのか、というような問題が生じる」と述べた上で、「私には、基本的関係が相対論的に不変で…あるから、そこにはそれほどの困難はないように思われる」^(*)と続けて、位置－運動量とともに時間－エネルギーの不確定性関係が成り立つことの重要性を示唆している。

(*)『ニールス・ボーア論文集１　因果性と相補性』（岩波文庫）p.92。引用したのは、「時空の連続性と原子物理学」（1931)という未公開草稿の一部だが、ここには、ボーアの（あまり練られていない）素朴な量子論解釈がいろいろと語られている。

　相対論的不変性を満たすように時間－エネルギーの間にも不確定性関係が成立するという主張は、不確定性を粒子・波動の二重性に起因する原理的なものであると見なす発想に根ざしている。ハイゼンベルグが不確定性の起源を観測者による系の不可避的擾乱にあると考えたのに対して、ボーアは、1927年のコモ講演^(*)で、電子のような粒子的存在が同時に波動として振舞うことによって、（人為的な観測による系の擾乱とは独立に）位置と運動量の不確定性が生じると主張した。コモ講演の内容を簡単に説明すると、次のようになる：物質粒子がΔｘ程度の拡がりを持った波動だとすると、重ね合わされている要素波の波の数は、（干渉条件を考えれば明らかなように）この範囲で１程度の変化を持っていなければならない。この関係を、波数ｋを使って表すと、
　　Δｘ・Δｋ～１
となる。波数と運動量の間のド・プロイの関係：ｐ＝ｈｋを利用すれば、
　　Δｘ・Δｐ～ｈ
という位置－運動量の不確定性関係を得る。

(*)『ニールス・ボーア論文集１　因果性と相補性』（岩波文庫）所収「量子仮説と原子理論の最近の発展」参照。ボーアが量子力学のマニフェストと言われる講演を行ったコモ会議は、1927年9月に開催されているが、アインシュタインは出席していない。また、この講演に基づく原稿が完成するのは1928年3月になってからなので、第５回ソルヴェイ会議の時点（1927年10月）では、アインシュタインは、コモ講演の内容に直接批判を加えられなかった。

　ボーアは、粒子・波動の二重性は量子論的なシステムにおける原理的な特徴だと見なしていたので、この関係式は（原理的な物理法則が常にそうあるべきなのと同様に）相対論的な不変性を満たしていると考えた。実際、物質粒子（電子など）の状態が波動で表されるとして、その時間的な拡がりをΔｔ、振動数の不定性をΔνとすると、
　　Δｔ・Δν～１
となり、ド・ブロイの関係：Ｅ＝ｈνを使えば、時間－エネルギーの不確定性関係が得られる。

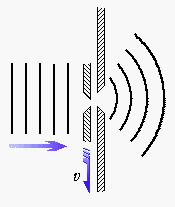後に、時間的な幅Δｔの意味を物理的に明確にするために、ボーアは、シャッターのついたスリットを持ち出し、Δｔをシャッターの開いている時間と解釈した。粒子が速度ｖで運動するシャッターの隙間を通り抜けるときに、横方向にΔｐの運動量をやり取りするならば、シャッターが得るエネルギーΔＥは、
　　ΔＥ～ｖΔｐ～ΔｑΔｐ／Δｔ～ｈ／Δｔ
という関係式を満たす（とボーアは考えた）ので、やはり時間－エネルギーの不確定性関係が成り立つことになる。この解釈は、1927年のソルヴェイ会議の際に、アインシュタインに提示されたようである。

　時間－エネルギーの不確定性関係に対するアインシュタインの反論は、量子力学的な不確定性が粒子・波動の二重性に起因するというボーアの基本的なアイデアを否定するものである。アインシュタインは、位置－運動量の不確定性関係が“現象論的に”満たされていることは認めていたが、これが原理的な関係式であるとは考えていなかった。時間－エネルギーの不確定性関係が成立しないことが示されれば、相対論的な不変性が満たされなくなるので、位置－運動量の不確定性関係が（原理的ではなく）現象論的な法則であるというアインシュタインの主張が立証されることになる。アインシュタインの批判が「ボーアにとって大変なショックで」あり、「もしもアインシュタインが正しいなら、物理学はもうお終いだ、と一人一人に説いてまわった」と伝えられるが、自分の立脚点が否定されることになるのだから、ボーアが深刻に受け止めたのも当然である。一方、ハイゼンベルグやパウリのような若手は、場の量子論という形式で量子力学を相対論的に不変にする手法を開発していたので、ボーアほどには衝撃を受けなかっただろう。
　実は、物理学的には、アインシュタインの主張は、大筋において正当なものである。位置と運動量の不確定性は、量子変数の力学的な性質（同時刻交換関係）に起因しているのであって、時空概念の適用不能性といった認識論的な根拠があるわけではない。より厳密に言えば、場の量子論における場の同時空交換関係を非相対論的に近似すると位置と運動量の不確定性関係が導出されるのである。この近似の範囲では、空間と時間の相対論的な関係は成り立っていないので、時間－エネルギーの間に原理的な不確定性関係は存在しない^(*)。

(*)科学史家は必ずしも明確に述べていないものの、このことは多くの物理学者がすでに指摘している。ただし、非定常系の場合には、時間とエネルギーの間に“不確定性関係もどき”が成り立つことも知られている。例えば、共鳴状態の寿命τと共鳴エネルギーの幅δＥの間には、τ・δＥ～ｈという関係がある。より一般的に、Ｒをあるエルミート演算子とし、ΔｔをＲの期待値がその間にＲの不確定さだけ変化する時間（Δｔ＝ΔＲ／｜ｄ＜Ｒ＞／ｄｔ｜）とすると、Δｔ・ΔＥ＞ｈ／４πなる関係が成立する（Mandelstam & Tamm；詳しい説明は、Ｍ．ヤンマー著『量子力学の哲学』などを参照されたい）。

　それでは、ボーアがコモ講演で示した議論は何を意味していたのか。かいつまんで言えば、位置－運動量の不確定性関係に関しては、非相対論的な交換関係：
　　［ｑ，ｐ］＝ｉｈ／2π　　（ｑ，ｐはエルミート演算子）
を初等的に解釈したものに他ならない。良く知られているように、この交換関係を満たすｐの固有状態をｑの固有状態を使って展開すると、
　　＜ｑ｜ｐ＞＝Ｃexp（－2πｉｑｐ／ｈ）
となる。自由運動している粒子の状態は、この関数の重ね合わせとして表される波束になるので、ｑとｐの拡がりの間にボーアが導いたような「不確定性関係」が成り立っている。しかし、時間の演算子は存在しないので、交換関係から時間とエネルギーの間の不確定性関係を導くことはできない^(*)。

(*)エネルギーが一定の値になる場合のシュレディンガー方程式の解は、
　　Ｃexp（2πｉＥｔ／ｈ）
という時間依存性を持っているので、その重ね合わせとなる波動関数にはボーアの議論が適用でき、エネルギーと時間の間に不確定性関係が成り立つように見える。だが、波動関数に現れる時間変数は、系の時間的変化を表すパラメータであって、物理的対象の「時間的拡がり」を記述するものではなく、ここから時間－エネルギーの不確定性関係を導くことはできない。ただし、コヒーレント光などのように、ある場所で観測したときの時間的変動が量子論的な効果に支配されている場合には、その時間的拡がりとエネルギーの間にある種の不確定性関係が成り立つことはある。

　興味深いことに、ボーアは、時間－エネルギー不確定性関係が原理的でないことを暴くきわめて巧妙なアインシュタインの思考実験を、“見事に”論破してしまった。これは、ボーアが論争のルールを勝手に変更したためであり、物理学的に正当な反論とは言い難い。このことを示すために、もう少し具体的に思考実験の内容を見ていこう。

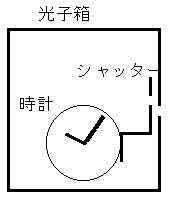　用意するのは、時計と連動したシャッターの付いた光子箱である（右図）。ある時刻Ｔに、短い時間間隔Δｔだけシャッターを開いて光子を放出する過程を考えよう。放出前後の光子箱のエネルギーは、質量を測定することによって正確に決定できる（放出の瞬間以外は、光子箱は熱的平衡状態にある定常系なので、エネルギーは確定している）。また、放出時刻は、シャッターを開いたときの時計の読みから決めることができる。この議論が巧妙なのは、時計も光子箱の中に入れられており、時計やシャッターを含むシステムが孤立系になっているので、エネルギーが外部からの擾乱されるという量子論特有の論法が使えない点である。従って、この過程が実現した時刻と移動したエネルギーは、いずれも不確定性なしに測定できることになり、時間－エネルギー不確定性関係が成り立っていないことが結論される。この主張は、シャッターを使った思考実験をもとに時間－エネルギーの不確定性を導き出すボーアの議論を踏まえながら、その論理的な欠陥を指摘するもので、不確定性が粒子・波動の二重性に由来する原理的なものだというボーアの主張の直接的な反例になっている。
　このアインシュタインの思考実験は、一般化することが可能である。エネルギーＥ₁の定常状態にあった系が、ある粒子を放出してエネルギーＥ₂の状態に遷移する場合を考える。このとき、放出前後の系のエネルギーと放出時刻は独立に測定することが可能なので、放出過程における時間－エネルギー不確定性関係は成立しない。このことは、原子の放射性崩壊の場合についてもあてはまる。アインシュタインが、こうした“わかりやすい”例を採用しなかったのは、1930年当時は核反応についての知見が十分でなく、放射性崩壊の過程でエネルギー保存則が成り立っているかも判然としていなかったからである（パウリがニュートリノ仮説を提唱し、β崩壊でもエネルギー保存則が満たされていることを示すのは1931年のことである）。また、アインシュタイン自身、原子核物理学についての知識は、あまり持ち合わせていなかった（1939年にシラードが核開発をルーズベルト大統領に進言する親書の署名を求めてアインシュタインのもとを訪れたとき、彼が核分裂の連鎖反応の可能性を知らなかったことに驚いている）。もっとも、エネルギーの測定が難しい光子箱を持ち出して反論の種を蒔いたことは、アインシュタインの失敗であった。

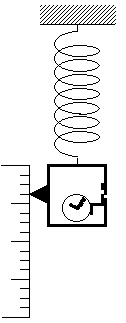　時間－エネルギー不確定性関係を否定する思考実験に対して、ボーアが試みた反論は、実に意表を付いたものだった。慣性質量を測定することによって（Ｅ＝ｍｃ²という相対論の関係式から）光子箱のエネルギーを決定するという実験の設定に対して、質量の測定を行うためには、光子箱を重力場内部の秤に吊り下げる必要があるため、一般相対論（重力理論）の影響を考慮しなければならないと切り返したのである。
　しかし、この反論は物理学的におかしい。まず、慣性質量の測定は、質量がわかっている粒子と衝突させるなどして測定することができるので、一般相対論を持ち出す必要はない（ただし、運動量の不確定性を考慮する必要が生じる）。そもそも、一般相対論に現れる質量は静止質量であって、運動エネルギーを繰り込んだ質量ではない（この点については、光子箱の反跳運動を考慮しなかったアインシュタインにも見落としがある）。また、量子力学は、一般相対論が成り立っていない仮想的なユークリッド空間の世界でも定式化できる（現にそのように定式化されている）はずであり、もともと含意されていない重力理論を持ち出すのは、理論の一貫性を無視した“ルール違反”である。
　さらに、ボーアの議論は、一般相対論の適用の仕方自体に問題がある。彼の議論の骨子は、次のようなものである。秤の位置（重量を表す目盛りの指す値でもある）ｑには、量子論的な不確定性Δｑがある。時計の進み方は重力場のポテンシャルに依存しており、重力加速度ｇの一様重力場内部では、時刻表示に、
　　ΔＴ＝ＴｇΔｑ／ｃ²
の不確定性が生じる。このΔＴと時計を含む系の質量の不確定性Δｍを結びつけようとして、ボーアは、重力に生じるｇΔｍの揺らぎが測定時間Ｔの間に系に力積を与え、運動量が最大ＴｇΔｍの揺らぎを被ると推測した。これをΔｐと置くと、位置と運動量の不確定性関係Δｑ・Δｐ～ｈより、Δｑには、
　　Δｑ＞ｈ／ＴｇΔｍ
と表される下限が生じる。これと上のΔＴの式を組み合わせれば、
　　ΔＴ＞ｈ／Δｍ・ｃ²
となり、ΔＥ＝Δｍ・ｃ²と置けば、時間とエネルギーの不確定性関係が導かれる。しかし、この議論では、バネからの復元力の寄与が正当に評価されていない。系は重力場内部で振動するため、力積は加算的には寄与せず、時計の進みと遅れも相殺される。何よりも、この議論を踏まえれば、質量が確定する（Δｍ＝0）と位置の不確定性が無限大になるという奇妙な結果が導かれてしまう。時間－エネルギー不確定性関係を思わせる式が導けたのは、全くの偶然だと言わざるを得ない。

　ボーアの反論が物理学的な正当性を欠いていたにもかかわらず、アインシュタインは、途中で論争を放棄してしまう。おそらく、アインシュタインは、的はずれの感のあるボーアの論旨に咄嗟に再反論ができなかったことに加えて、何としても自説を守り抜こうとするあまりに頑なな態度にいささか辟易し、それ以上の論争を続ける意欲が萎えたのだろう。このため、外見上はアインシュタインが論争に敗れた形になったが、実質的には、このラウンドは彼が勝利していたのである。

ＥＰＲ（アインシュタイン－ポドルスキー－ローゼン）論文(1935)
　アインシュタイン／ボーア論争の第３ラウンドは、有名なＥＰＲ論文を巡る攻防である。この議論に関しても、私は、アインシュタイン側が優勢であり、ボーアのきわめて晦渋な反論は物理学的に受け入れがたいと考えている。しかし、ＥＰＲの議論については、膨大な論文が執筆され、いくつかの決定実験も遂行されているので、この小論で論じるにはいささか荷が重く、別の機会に譲ることにする。

【追記】ＥＰＲの議論については、下記の論文で議論している。
　　論文「ＥＰＲ論文を巡って」

【「科学の回廊」目次に戻る】